ЕЩЕ РАЗ О СИНХРОНИЗАЦИИ ЧАСОВ
В СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
Ю.И.Наберухин
Одним из важнейших
выводов, который следует из специальной теории относительности (СТО) и получил
всеобщее распространение, является тезис об относительности одновременности.
Обычно он связывается с проблемой синхронизации часов, находящихся в разных
точках пространства. Именно с описания процедуры синхронизации часов
начинается, как известно, первая статья А.Эйнштейна [1], в которой изложены
основы СТО. Уже сам Эйнштейн подчеркивал, что предлагаемая им процедура
синхронизации есть определение, т.е. не является однозначной и
обязательной. Однако создатель теории относительности не разъяснял (очевидно,
понимая, что это не относится к физическому содержанию развиваемой концепции),
как изменится формализм СТО и как интерпретировать эти изменения, если принять
какое-либо другое, отличное от предложенного им, определение синхронизма.
Эта проблема была
впервые рассмотрена Г.Рейхенбахом [2]. Он предложил
более общее условие синхронизма и с его помощью указал возможные границы
произвола, которые якобы имеются в определении одновременности. С момента
выхода в 1928 г. книги Рейхенбаха его рассуждения
стали непременно включаться – без какой-либо критики, а скорее, как важный
вклад в основы теории относительности – в трактаты по философии
пространства и времени (назовем для примера книги Г.Рейхенбаха [3], А.Грюнбаума
[4], Ю.Б.Молчанова [5]), и идея конвенциального характера определения
одновременности получила всеобщее распространение. Характерно, что в
философской литературе совершенно не затрагивается вопрос о том, как изменится
формализм СТО, если принять другое, не эйнштейновское, определение одновременности.
Между тем совершенно, на наш взгляд, правильное и ясное решение этого вопроса
было дано А.А.Логуновым [6], который показал, что на
самом деле никакого произвола в определении одновременности нет. Это заключение
осталось незамеченным в философской литературе, видимо, потому, что не все
философы свободно разбираются в физических рассуждениях и математических
выкладках.
В настоящей статье
мы, по существу, повторяем выводы Логунова, но делаем
это несколько иным способом. Мы идем по пути Эйнштейна, который в своей первой
статье при выводе преобразований Лоренца существенно использовал свою процедуру
синхронизации часов, что встречается только в этой работе и никогда не
применялось в других многочисленных способах их вывода. Мы прослеживаем, как
изменятся выкладки Эйнштейна, если использовать "обобщенное" условие
синхронизма по Рейхенбаху. Это позволяет прояснить
истинное место проблемы синхронизации часов в СТО.
Синхронизация часов по Эйнштейну и Рейхенбаху
Пусть мы хотим
синхронизовать часы, которые находятся в одной и той же системе отсчета в
точках х1
и х2 на
расстоянии l по оси Х. Процедура Эйнштейна заключается в том, что из точки х1 в момент t1 по
часам, находящимся в этой точке, выпускается световой сигнал, который
отражается от зеркала в точке х2 и приходит обратно в точку х1 в момент t3 (см.
рисунок). Тогда на часах в точке х2 в момент
прихода туда сигнала нужно установить время t2 по рецепту
![]() (1)
(1)
Это, очевидно,
подразумевает, что свет распространяется туда и обратно с одной и той же
скоростью. Рейхенбах полагает, что условие
синхронизма (1) «не является эпистемологической
необходимостью» и его можно заменить «некоторым произвольным правилом» [7]
![]() (2)
(2)
Параметр ε должен
удовлетворять условию ![]() , чтобы выполнялась
естественная последовательность моментов t1 < t2
< t3. В
остальном же значение ε , по
мнению Рейхенбаха, совершенно произвольно. Ясно, что
параметр ε выражает анизотропию скорости света по оси Х. Если
обозначить через с+ скорость
света в положительном направлении оси Х, а через с– (c–
> 0) – в противоположном
направлении, то будет справедливо
, чтобы выполнялась
естественная последовательность моментов t1 < t2
< t3. В
остальном же значение ε , по
мнению Рейхенбаха, совершенно произвольно. Ясно, что
параметр ε выражает анизотропию скорости света по оси Х. Если
обозначить через с+ скорость
света в положительном направлении оси Х, а через с– (c–
> 0) – в противоположном
направлении, то будет справедливо
t2 = t1 + l/c+ , t3 = t2 + l/c– . (3)
После
исключения отсюда l получаем из (2)
ε = с– /( c+
+ c–) . (4)
Эйнштейн
постулировал, что свет распространяется изотропно: c+
= c– = с, –
и поэтому у него ε = ½ .
“Обобщенные” преобразования Лоренца
Проследим теперь
рассуждения Эйнштейна, ведущие к преобразованиям Лоренца, заменяя его рецепт
синхронизации часов (1) на "обобщенный" (2). Математические выкладки
вынесены в Приложение, а здесь наметим общую логику метода Эйнштейна, который
никто впоследствии не использовал [8]. Сначала Эйнштейн синхронизирует часы в
инерциальной системе отсчета S’, движущейся со скоростью v относительно системы S вдоль оси Х.
Подставляя условие синхронизации (2) в искомое линейное преобразование от нештрихованных координат системы S к штрихованным в системе S’ , получим
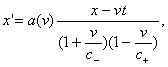 ®
®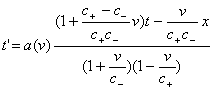 , (5)
, (5)
где
a(v) – некоторая
неизвестная функция скорости (в статье Эйнштейна, естественно, было c+ =
c– = c).
Для определения этой
функции Эйнштейн описывает распространение света по оси Y. Но какова
скорость света по оси Y? У Эйнштейна было все просто: при изотропном
распространении света его скорость по всем направлениям одинакова. Теперь же на
этот вопрос невозможно ответить без дополнительных постулатов. Весьма неразумно
придумывать эти постулаты ad hoc, нанизывая одни неочевидные аксиомы на другие,
как это делает, например, Дж.Уитроу,
пытаясь доказать неизбежность рецепта (1) [9]. На все подобные вопросы легко
получить ответы, если правильно сформулировать сущность СТО, которая и будет
выступать как генеральный постулат.
Сущность же
специальной теории относительности как физической теории пространства и
времени, несомненно, заключается в том, что она утверждает: пространственные
и временные координаты образуют единое четырехмерное многообразие с
псевдоевклидовой геометрией. Математически это означает, что существует
система координат (ее разумно называть лоренцевой), в
которой пространственно-временное многообразие имеет метрику вида
ds2
= c2dt2 – dx2 – dy2 –
dz2 (6)
и
которая инвариантна относительно некоторой группы
преобразований многообразия самого в себя [10]. Физическая интерпретация этого
пока еще математического утверждения заключается в том, что (i) такая метрика соответствует инерциальной системе отсчета
(с прямоугольной декартовой системой координат); (ii) существует бесконечно
много инерциальных систем, движущихся друг относительно друга с постоянной
скоростью v; (iii) координаты любых двух инерциальных систем
связаны определенными преобразованиями (преобразованиями Лоренца), оставляющими
инвариантной метрику (6) [11]. То, что эти преобразования образуют группу
(параметром которой является скорость v), можно считать математическим изыском, и мы не
используем это свойство в дальнейших рассуждениях [12].
Из условия
инвариантности метрики относительно преобразований (5) легко определить
неизвестную функцию a(v). Для
этого полагаем, как всегда, dy’=dy, dz’=dz и пишем
условие инвариантности метрики в виде
At’2
+ Bx’t’ – x’2 = At2 + Bxt – x2
(при
анизотропном распространении света квадратичную форму, описывающую метрику,
нужно записывать в общем виде, т.е. с недиагональным членом). Подставляя сюда
(5), после простых, но длинных вычислений найдем неизвестные коэффициенты A , B и функцию a(v):
A = c+c– ,
B = c+ – c– ,
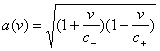 . (7)
. (7)
Таким образом,
метрика имеет вид
ds2
= c+c–dt2 + (c+ – c–)
dxdt – dx2 – dy2 –
dz2 , (8)
а
преобразования (5) с учетом (7) приобретают более сложную форму по сравнению с
обычными преобразованиями Лоренца, переходя в них при c+ =
c– = с.
Заметим, что формулы
(7) и (8) можно получить и другими способами [13]. В частности, они следуют из
требования о том, чтобы преобразования между системами отсчета S и S’ образовывали
группу [14].
Смысл "обобщенной"
синхронизации
Математическое
содержание формулы (8) состоит в том, что она описывает псевдоевклидову метрику
четырехмерного пространства-времени в косоугольных прямолинейных (коэффициенты
в (8) постоянны) координатах, в которых ось Т неортогональна
оси Х. Таким
образом, предположение о неравенстве скорости света вперед и назад по оси Х (c+
≠ c–) приводит лишь
к тому, что от ортогональной лоренцевой системы
координат, в которой записана метрика (6), мы переходим к неортогональной
системе координат, в которой метрика принимает вид (8).
Следует
иметь в виду, что всегда можно сконструировать такую систему координат (вообще
говоря, криволинейную неортогональную), в которой
скорость света будет выражаться любой наперед заданной функцией
пространственных и временной координат. Однако здесь речь может идти только о "координатной
скорости", а не об истинной "физической" скорости света, которая
в рамках СТО во всех направлениях одна и та же и равна с. Для установления связи между
координатными и физически осмысленными величинами имеется простой рецепт [15]
(который сохраняется и в искривленном пространстве-времени общей теории
относительности). От выбранной нами системы координат (которая может быть
любой) нужно перейти к новым координатам, таким чтобы метрика в данной точке
пространства и в данный момент времени имела форму (6), т.е. нужно представить
ее в виде
ds2 = c2dt2 - dl2.
Физически это
означает, что мы переходим в инерциальную лоренцеву
систему отсчета, локально совпадающую с той, в которой мы
работаем. Только в такой форме координаты имеют ясный
физический смысл: t –
это "истинное", собственное время, а l –
"физическая", т.е. измеряемая реальными "твердыми"
линейками длина. Здесь с – уже "истинная", т.е. не
координатная, скорость света. Переход к этой форме однозначен и в нашей метрике
(8) дается формулами
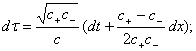 ®
®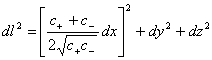 .
.
Физическая скорость
по оси Х теперь есть
Vxphys = dlx/dt , и она выражается через координатную скорость vx = dx/dt довольно
громоздкой формулой [16]
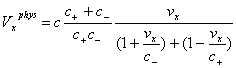 .
.
Подставляя сюда в
качестве координатной скорости скорость света с+ , т.е. vx = с+ , получим Vxphys = с, а координатной
скорости –с– соответствует Vxphys = –с. Таким образом,
неравные друг другу скорости света (c+
≠ c–), которые были
положены в основу рассуждений о произвольности синхронизации часов, – это
всего лишь "координатные скорости", неявно подразумевающие описание
в специальной (неортогональной) системе координат.
Основной постулат СТО об изотропном характере (пустого) пространства-времени
этим нисколько не затрагивается, так что истинная, "физическая"
скорость света во всех направлениях остается одинаковой.
Итак, рецепт
синхронизации часов Эйнштейна условен лишь в той же мере
в какой условен выбор той или иной системы координат. Поэтому никакой эпистемологической
конвенциальности в этом рецепте нет. Можно говорить
разве только о математической конвенциальности,
условности или необязательности. Никаких философских глубин в такой условности
усмотреть нельзя: она обычна для математического формализма, который является
гибким инструментом в руках исследователя, вольного выбирать инструмент (в
данном случае – систему координат [17]), удобный для его задач и для его
способов действия.
Почему в обычных выводах преобразований
Лоренца
не используются процедуры синхронизации часов
Все признают, что
анализ одновременности, начинающийся с проблемы синхронизации часов, является
важнейшим нововведением Эйнштейна. Действительно, без предварительной
синхронизации часов невозможно ни описать движение, ни установить закономерности
пространства-времени. Поэтому понятно, что при выводе преобразований Лоренца,
которые выражают важнейший момент этих закономерностей, Эйнштейн исходит из
условия синхронности. Но тогда возникает два вопроса. Во-первых, нужно
объяснить, как удается обойтись без предварительного установления синхронности
часов во всех способах вывода преобразований Лоренца, предложенных после первой
работы Эйнштейна, которые можно найти в любых учебниках или трактатах по теории
относительности. Во-вторых, очевидно, что и в нерелятивистской физике описание
движения совершенно невозможно без синхронизации часов. Почему же и после
Эйнштейна о синхронизации ничего не говорится ни в классической механике, ни в
классической электродинамике [18]?
На оба этих вопроса
есть один простой ответ. И при выводе преобразований Лоренца, и везде в
классической физике синхронизация часов осуществляется неявно – через
понятие скорости. Действительно, скорость перемещения какого-либо объекта из
места с координатой х1 (для
краткости – из точки х1) в точку
х2 есть
v = (х2 – х1)/(t2 –
t1), (9)
где
t1 и t2 –
показания часов в точках х1 и х2. Ясно, что это выражение имеет смысл, только если
часы в двух точках синхронизованы, иначе величина скорости могла бы иметь
произвольное значение. Поэтому когда мы говорим о скорости, мы подразумеваем,
что часы в соответствующих точках пространства синхронизованы. Из определения
скорости (9) следует и рецепт синхронизации:
t2 = t1 + l/v , (10)
где
l = х2 –
х1 – расстояние
между двумя точками, измеренное в той же системе отсчета, в которой покоятся
часы. Это очевидное соотношение использовал сам Эйнштейн – независимо от
процедуры синхронизации (см. Приложение, где оно неоднократно фигурирует), его
же имели в виду и мы, когда писали формулы (3). Только там описывалось
распространение света, но формулы (9) и (10), конечно, верны для любых
движений.
Против этих
рассуждений имеется традиционное возражение. Считается, что нельзя говорить о
скорости, если не указан рецепт ее измерения. Но рецепт (9) уже требует
синхронизации часов. Таким образом, мы получаем порочный круг: рецепт
синхронизации (10) требует знания скорости, а знание скорости требует наличия
синхронизованных часов. Однако это возражение имеет силу только в рамках
формальной логики [19]. Проблема же структуры пространства-времени, которую мы
обсуждаем, – это отнюдь не логическая проблема. Здесь мы не можем обойтись
без понятия движения и понятия скорости, которая есть количественная мера
движения. Как измерить эту скорость – совсем другой вопрос. И как бы мы на
него ни отвечали, мы до всякого измерения можем вводить понятие скорости
рассматриваемого процесса, которая имеет объективное содержание и некоторое
численное значение.
Что касается способа
измерения скорости, то это тоже не логическая проблема и ее нужно решать
посредством не конвенции, а содержательных физических соображений. Таковыми
являются законы природы, отображаемые в физических теориях [20]. В механике это
законы Ньютона. Зная характер действия сил, мы можем при помощи второго закона
рассчитать скорость и без непосредственного ее измерения. Первый закон
эквивалентен утверждению, что две инерциальные системы отсчета движутся друг
относительно друга с постоянной скоростью. Если бы до измерения величины
скорости о ней нельзя было бы говорить, то невозможно было бы поставить сам
вопрос о принципе относительности. Ведь все рассуждения о принципе
относительности (как Галилея, так и Эйнштейна) начинаются с констатации: две
инерциальные системы отсчета движутся друг относительно друга со скоростью
v. Почему же при этом никто не спрашивает, как измерить данную скорость,
и этот вопрос возникает только при синхронизации часов?
Известные рассуждения
о том, что скорость света в одном направлении невозможно измерить, верны также
только в рамках формальной логики. Говорят, что Эйнштейн постулировал
в СТО, что скорость света во всех направлениях одна и та же. Да, это было
постулатом при генезисе теории. Но теперь, когда теория относительности
является общепринятой основой современной физики, это положение нужно считать
законом природы. Мы видели, что попытки "обобщить" постулат Эйнштейна
сохраняют в силе этот закон. Он, разумеется, относится к
"физической", а не к координатной скорости.
Впрочем, этот закон
был известен и до теории относительности. Он содержится в электродинамике
Максвелла, которая (будучи лоренц-инвариантной)
осталась справедливой и в релятивистской физике. В теории Максвелла
электромагнитные волны распространяются изотропно и их скорость равна отношению
так называемых электромагнитной и электростатической единиц. Последнее
означает, между прочим, что скорость света в одном направлении
можно узнать без измерения световых сигналов, из статических электрических и
магнитных измерений – разумеется, на основе теории, которая является выражением
объективных законов природы.
Итак, коль скоро мы
оперируем понятием скорости, нам не нужно заботиться о синхронизации часов. Это
положение настолько интуитивно очевидно, что оно не оговаривается ни в
классической (дорелятивистской) физике, ни в теории
относительности при обычных выводах преобразований Лоренца. Значение процедуры
синхронизации часов в СТО сильно преувеличено. Эйнштейну эта процедура была
нужна для того, чтобы сделать убедительными и бесспорными удивительные
заключения об относительности одновременности, сокращении длин и замедлении
часов. Операциональный подход оказывается очень
эффективным для прояснения тонких вопросов. Однако операциональные
«леса» не нужно путать с сущностью теории. Когда эта сущность выяснена, «леса»
можно разобрать.
Можно ли обойтись без свойств света при синхронизации часов
Из только что
сказанного ясно, что, вопреки расхожему мнению,
свойства света совершенно необязательно использовать при обсуждении проблемы
синхронизации часов и одновременности. Об этом говорил и сам Эйнштейн: «Чтобы
придать понятию времени физический смысл, нужны какие-то процессы, которые дали
бы возможность установить связь между различными точками пространства. Какого
рода процессы выбираются при таком определении времени, несущественно… Распространение
света в пустоте… подходит для этой цели в гораздо большей степени, чем любой
другой процесс» [21].
Использовать свет
наиболее удобно, когда речь идет о сравнении событий в разных
инерциальных системах отсчета, ибо скорость света инвариантна относительно
преобразований координат. Однако если речь идет о синхронизации часов в одной
системе отсчета, то здесь распространение света не имеет никаких преимуществ по
сравнению с другими процессами. Мы можем использовать любое движение с постоянной
скоростью v и синхронизовать часы при помощи рецепта (10),
установив, например, в точке х2 время t5 = t4 + l/v, начав наше движение из точки х1 в момент t4 (см.
рисунок). Установленная таким образом синхронизация часов в точках х1
и х2 будет сохраняться и в последующие моменты времени,
поскольку "ход часов" в этих точках одинаков [22]; в этом можно будет
убедиться, например, при помощи процедуры Эйнштейна (см. рисунок).
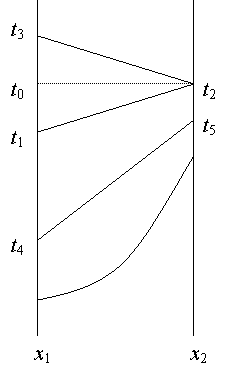 Предельность скорости света также не имеет значения
для синхронизации часов. Процедура (10) будет работать и для сверхсветовых
движений (тахионов [23])., если они вдруг будут открыты. Более того, описанный
рецепт синхронизации дает правильный результат и для сигналов,
распространяющихся с бесконечной скоростью, если бы такие существовали. Этому
случаю соответствует траектория t0 – t2 на
рисунке, причем t2 = t0
= ½(t1 + t3), т.е. бесконечно быстрый сигнал осуществляет рецепт
синхронизации Эйнштейна (1). Для синхронизации часов необязательно использовать
сигналы, распространяющиеся с постоянной скоростью. Синхронизацию по рецепту
(10) можно осуществить любым процессом (см. нижнюю часть рисунка), если
известен закон его временной эволюции v
= v(t):
Предельность скорости света также не имеет значения
для синхронизации часов. Процедура (10) будет работать и для сверхсветовых
движений (тахионов [23])., если они вдруг будут открыты. Более того, описанный
рецепт синхронизации дает правильный результат и для сигналов,
распространяющихся с бесконечной скоростью, если бы такие существовали. Этому
случаю соответствует траектория t0 – t2 на
рисунке, причем t2 = t0
= ½(t1 + t3), т.е. бесконечно быстрый сигнал осуществляет рецепт
синхронизации Эйнштейна (1). Для синхронизации часов необязательно использовать
сигналы, распространяющиеся с постоянной скоростью. Синхронизацию по рецепту
(10) можно осуществить любым процессом (см. нижнюю часть рисунка), если
известен закон его временной эволюции v
= v(t):
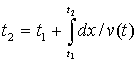 .
.
Разумеется, этот
закон нельзя найти средствами логики. Но физика и другие точные науки умеют это
делать.
Заключение
Итак, теория
относительности не вносит ничего нового в кинематику (не в динамику!) по
сравнению с классической физикой, коль скоро мы находимся в одной системе
отсчета. Все рассуждения о синхронизации часов и одновременности и там,
и там ничем не различаются. Распространение света ничем не выделено среди всех
других процессов. В частности, предельность скорости света также не имеет
никакого значения в этих рассуждениях. Поэтому в рамках одной инерциальной
системы отсчета и в теории относительности можно говорить об абсолютном
пространстве и времени, общем для всех точек пространства (разумеется, здесь
речь идет о пустом плоском пространстве-времени, свободном от гравитации).
Ситуация существенно
меняется, когда мы хотим перейти в другую систему отсчета, движущуюся
относительно данной. Для описания такого перехода
недостаточно логических рассуждений, – совершенно
необходимо опираться на законы природы. И наиболее удобно здесь использовать
закон инвариантности описания распространения света во
всех инерциальных системах отсчета. Это утверждение не есть постулат или
конвенция (так можно было бы говорить только с точки зрения формальной логики),
это истинный объективный закон природы, верифицируемый
всем опытом современной физики. В свете данного закона принцип относительности
выступает как требование лоренц-инвариантности
математической формы законов природы. Однако форма этих законов, как и самих
преобразований Лоренца, имеет разный вид в разных системах координат (которые
можно выбирать как угодно), используемых в инерциальных системах отсчета.
Разный вид при этом получают и процедура синхронизации часов, и условие
одновременности удаленных событий. Но никакого философского или эпистемологического содержания в этом математическом обстоятельстве
усмотреть нельзя. Длинные рассуждения по этому поводу, которые предпринимают Рейхенбах и его последователи, отнюдь не
"обогащают" [24], а только запутывают проблему синхронизации часов и
относительности одновременности.
![]() Приложение
Приложение
Вывод преобразований Лоренца по
Эйнштейну
Повторим в несколько
модернизированном виде способ вывода преобразований Лоренца, как он дан в
первой работе Эйнштейна, но с заменой рецепта синхронизации Эйнштейна на рецепт
Рейхенбаха. Пусть дана покоящаяся инерциальная система
отсчета S (x,y,z,t) и движущаяся относительно нее по оси X с постоянной скоростью v система S' (x',y',z',t'). Искомые
преобразования «должны быть линейными в силу свойства
однородности, которое мы приписываем пространству и времени» (в кавычках даются
цитаты из работы Эйнштейна). Поэтому для преобразования времени напишем
t' = t'(x*, t) = bx* +
at , (П1)
где коэффициенты a и b зависят только от скорости v. Здесь x* = x – vt ; «ясно, что точке, покоящейся в системе S', будет принадлежать определенный, не зависящий от времени набор значений x*, y, z ». (Введение точки x* – хотя маленький, но тоже оригинальный момент метода Эйнштейна.)
Теперь синхронизируем часы, находящиеся в некоторой фиксированной точке x'2 движущейся системы S', соответствующей точке x* неподвижной системы S, с часами, находящимися в начале координат системы S'. Для этого из начала координат системы S' (соответствующем точке x* = 0 системы S ) посылаем луч света вдоль оси X в точку x* (в момент t по часам в S ); этот момент по часам в S' есть t'1 [0, 0, 0, t], причем в квадратных скобках здесь и далее указаны координаты события в системе S. Пусть этот луч отразится от зеркала в точке x'2 в момент t'2 и возвратится в начало координат системы S' в момент t'3 . С точки зрения системы S свет проходит путь x* от начала координат до точки x* за время x*/(c+ – v) , а обратный путь за время x*/(c– + v). Поэтому t'2 = t'2[x*, 0, 0, t + x*/(c+ – v)] и t'3 = t'3[0, 0, 0, t + x*/(c+ – v) + x*/(c– + v)].
По условию
синхронизма Рейхенбаха (2) должно быть
t'2 = (1 – ε) t'1 + ε t'3 .
Выражая координаты событий
посредством (П1) и имея в виду (4), получим отсюда
соотношение ![]() . Из (П1) тогда имеем
. Из (П1) тогда имеем
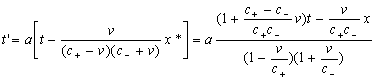 (П2)
(П2)
Здесь мы учли определение x* = x – vt
Для закона распространения света, испущенного из начала координат в положительном направлении оси X, в системе S' имеет место x' = c+t' (скорости света c+ и c– инвариантны, т.е. одинаковы в S и S'). "Но относительно начала координат системы S' луч света при измерении, произведенном в покоящейся системе, движется со скоростью с+ – v, вследствие чего x*/(c+ – v) = t (у Эйнштейна, разумеется, вместо c+ было с. – Ю.Н.). Подставляя это значение t в уравнение для x', получим", учитывая (П2) и определение x* = x – vt
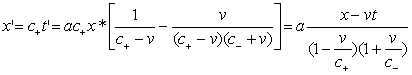 . (П3)
. (П3)
Соотношения (П2) и (П3) дают искомые преобразования с точностью до коэффициента a – некоторой функции скорости v.
Для определения этой
функции Эйнштейн рассматривает движение света вдоль оси Y,
испущенного из начала координат системы S'. Тогда y'=ct'=cat ; последнее равенство следует из (П2) при x* = 0. С точки зрения системы S свет движется по закону y=(c2 –
v2)1/2 t, который вытекает из теоремы
Пифагора: свет, проходя путь ct, распространяется по гипотенузе прямоугольного
треугольника, катетами которого являются проекция этого пути на ось X (vt) и искомая
проекция на ось Y (y).
Таким образом, t = (c2 – v2)–1/2
y. Подставляя это в формулу
для y', будем иметь y'
= ac(c2 – v2)–1/2y. Полагая y'
= y, получаем для искомой функции: a = (1 –
v2/c2)1/2.
Эта процедура
Эйнштейна дает решение задачи только для изотропного распространения света. Для
анизотропного случая она не проходит по двум причинам. Во-первых, неясно, как
выражается (координатная) скорость распространения света по оси Y через c+ и c– .
Во-вторых, в анизотропном пространстве-времени не обязана выполняться теорема
Пифагора. Мы не беремся составить систему аксиом, которые бы a priori позволили
ответить на эти вопросы. Но ответы легко получаются из метрики (8),
соответствующей анизотропному распространению света вдоль оси X. В системе
S', где dx' = dz' = 0, из условия
распространения света ds' 2 = 0 имеем cy
= dy'/dt' = (с+с_)1/2 и, значит, по процедуре Эйнштейна, y' = cy t' = acy
t. В системе S, где dx/dt = v, dz
= 0, имеем ds2 = dt2[c+c–
+ (c+ – c–)v – v2 –
(dy/dt)2]
= 0 и значит y = [c+c–
+ (c+ – c–)v – v2]1/2
t. Поэтому y' = a(c+c–)1/2
[c+c– + (c+ – c–)v –
v2]–1/2 y, откуда при y'
= y следует выражение (7) для функции
а.
Примечания
1. См.: Эйнштейн
А. К электродинамике движущихся тел // Эйнштейн А. Собрание
научных трудов. – М., 1965. – Т. 1. – С.7; см. также: Принцип
относительности. – М., 1973. – С.97.
2. См.: Reichenbach
H. Philosophie der Raum-Zeit-Lehre. – B., 1928.
3. См.: Рейхенбах Г. Философия пространства и
времени. – М., 1985.
4. См.: Грюнбаум А. Философские проблемы пространства
и времени. – М., 1969.
5. См.: Молчанов
Ю.Б. Четыре концепции времени в философии и физике. – М., 1977.
6. Краткое изложение
см. в послесловии А.А.Логунова к книге Г.Рейхенбаха «Философия пространства и
времени» и в подробностях – в книге самого Логунова
«Лекции по теории относительности и гравитации» (М., 1987). Замечу, что я
полностью согласен со всем, что говорится Логуновым о
сущности СТО, и считаю его книгу наиболее ясным изложением тонкостей ее
формализма, но не согласен с оценкой вкладов Г.А.Лоренца и А.Пуанкаре в
создание СТО и не разделяю данной Логуновым критики
общей теории относительности и попыток ее замены "релятивистской теорией
гравитации".
7. Рейхенбах Г. Философия пространства и
времени. – С.147.
8. Любопытно, что при
первой публикации статьи Эйнштейна на русском языке в сборнике «Принцип
относительности» (М., 1935) его редакторы В.К.Фредерикс
и Д.Д.Иваненко сделали примечание (на с.146), что преобразования Лоренца можно
вывести проще, чем здесь это делает Эйнштейн, – прямо из условия инвариантности закона распространения света. Это замечание к
классической работе совершенно неуместно своей антиисторичностью и в дальнейших
публикациях, к счастью, не повторялось (см., например, книги, указанные в прим. [1]). Но оно знаменательно тем, что демонстрирует
нежелание разбираться в логике рассуждений Эйнштейна. Это нежелание широко
распространилось в среде как физиков, так и философов
(не говоря уже о дилетантах), что часто приводит к заключению об "ошибках
Эйнштейна". Отметим кстати, что в фундаментальном четырехтомном «Собрании
научных трудов» Эйнштейна таинственным образом исчезло важное примечание самого
Эйнштейна: «Имеется в виду “действительны в первом приближении”» (т.1,
с.8 – после первой фразы в §1 о справедливости уравнений механики Ньютона).
Это досадное упущение повторено в издании: Эйнштейн А. Теория
относительности: Избранные работы. Ижевск, 2000.
9. См.: Уитроу Дж. Естественная философия
времени. – М., 1964. – С.240–251.
10. Как известно,
согласно Эрлангенской программе Ф.Клейна, которая
установила современный взгляд на математическую сущность геометрии, каждый вид
геометрии определяется своей специфической группой автоморфизмов, т.е.
преобразований пространства самого в себя. Хорошее популярное обсуждение этих
вопросов можно найти в статьях А.Д.Александрова и А.И.Мальцева в третьем томе
компендиума "Математика, ее содержание, методы и значение" (М.:
Изд-во АН СССР, 1956).
11. В формулировке сущности СТО мы следуем А.А.Логунову,
который несколько раз повторяет ее в упомянутой в прим. [6] книге (с. 25, 30,
37). Далее он продолжает: «…Принцип относительности, по существу,
представляет собой лишь тривиальное проявление псевдоевклидовой геометрии
физического пространства-времени, не более». Это верно именно по существу, но
не по форме, ибо из псевдоевклидовости самой по себе
отнюдь не следует эквивалентность инерциальных систем отсчета.
Математическая форма тезиса о псевдоевклидовости
пространства-времени должна быть дополнена физическим содержанием, что мы и
делаем в пунктах (i)–(iii). Именно совмещение
физической постановки вопроса (Эйнштейн) с адекватной математической
формулировкой (Минковский) привело к революционному
прорыву в философии пространства и времени.
12. О групповом
характере преобразований Лоренца упомянуто уже в первых статьях Эйнштейна (с
пометкой «как это и должно быть») и Пуанкаре («важно отметить, что
преобразования Лоренца образуют группу»).
13. См., например, упомянутую в прим. [6] книгу А.А.Логунова.
14. Вывод преобразований Лоренца на основе теории непрерывных групп впервые
сделан в статье Ф.Франка и Г.Рота «О преобразовании пространственно-временных
координат для медленно движущихся систем» (см.: Frank Ph., Rothe H. Über die
Transformation der Raumzeitkoordinaten
von ruhenden auf bewegte Systeme // Ann.d.Phys. –
1911. – Bd. 34. – S.825–855). Упрощенный и очень ясный вариант этого вывода (в предположении изотропности пространства по оси Х) дан в лекциях по
теории относительности Л.И.Мандельштама (см.: Мандельштам Л.И. Полное
собрание трудов. – М., 1950. – Т. V. – С.281–302; Он
же. Лекции по оптике, теории относительности и квантовой механике. –
М., 1972. – С.261–282). Групповой вывод
преобразований Лоренца, основывающийся на мощном аппарате дифференциальных
уравнений С.Ли (которым должны удовлетворять преобразования координат, если
они составляют группу), обладает важными методологическими преимуществами.
Во-первых, он исходит не из инвариантности метрики, а только из линейности
преобразований; инвариант может быть установлен позже. Во-вторых, в нем не
используются никакие свойства света; параметры c+ и c–
появляются в нем как формальные неопределенные константы, физический
смысл которых должен быть установлен дополнительно. Таким образом, требование групповости является наиболее сильной аксиомой при выводе
преобразований Лоренца, которая одна заменяет множество других, обычно вводимых
для этой цели.
15. См. упомянутую в прим. [6] книгу А.А.Логунова
или учебник Л.Д.Ландау и Е.М.Лифшица "Теория поля" (М.: Наука,
1973. – § 84).
16. Сложные по виду
формулы, которые мы здесь приводим, казалось бы, неуместны при обсуждении
философских методологических вопросов. Однако спорные проблемы СТО невозможно
серьезно обсуждать, не разбираясь в конкретной математике. Иначе все
превращается в общие слова, не имеющие доказательной силы.
17. Здесь особенно
ясно отличие системы отсчета от системы координат. Система
отсчета – это некоторое "твердое тело", относительно которого мы
рассматриваем движение (или, вообще говоря, физическое явление). Она однозначно
определена постановкой задачи: в нашем случае имеются две системы отсчета S и
S’, связанные с двумя твердыми телами, движущимися по инерции с
относительной скоростью v. Но в каждой из этих систем отсчета можно
выбрать разные системы координат (т.е. способы оцифровки пространства и времени), –
это могут быть либо декартовы координаты, либо полярные, либо какие угодно
другие. Системы координат могут быть даже разными в двух системах отсчета: в
них могут использоваться разные масштабы для измерения пространства и времени и
разные условия синхронизации часов. Такие допущения делает Рейхенбах
(с.167 его книги, упомянутой в прим.
[3]) и вслед за ним Грюнбаум (с.452 книги, упомянутой
в прим. [4]), пытаясь показать на основе якобы философской допустимости
значений ε ≠ ½, что относительность одновременности
в СТО не является необходимой и что вывод об относительности одновременности
есть ошибка в интерпретации СТО. Однако введение ε ≠
½, как мы показали, – это чисто математический трюк, означающий
переход в косоугольную систему координат. В ней математические соотношения,
конечно, другие, чем в прямоугольной лоренцевой. Но это только запутывает обсуждение проблемы;
во всяком случае, никакой философской или эпистемологической
нагрузки в таком усложнении нет. Сама постановка вопроса о возможности восстановления
одновременности в движущейся системе отсчета путем введения ε ≠
½, т.е., в нашей интерпретации, путем наклона оси Т
к оси Х, очень странная. Она делает невозможной формулировку принципа
относительности. Ведь значение ε ≠ ½ зависит от
скорости движения этой системы, а значит, каждой движущейся системе отсчета мы
должны приписать свою особую систему координат, что исключает их
равноправность.
18. Иногда приходится
слышать такой ответ на этот вопрос: в ньютоновской
механике время абсолютно и в любой точке одинаково, поэтому и не нужно
синхронизовать часы. Но в рамках проблемы синхронизации часов речь идет о другом: как, какой
процедурой установить часы в разных точках так, чтобы они показывали это
абсолютное время. Если это важно в СТО, то это важно и в классической механике.
19. См.: Рейхенбах Г. Философия пространства и
времени. – С.146–147. Далее автор продолжает: «Сам факт наличия порочного
круга свидетельствует о том, что одновременность есть вопрос не познания, но координативной дефиниции и что установление одновременности
в принципе невозможно» (с.147). Такого рода категорические, но ложные
утверждения, которыми переполнены книги Рейхенбаха и Грюнбаума, появляются из-за того, что авторы полагают, что
они в своем анализе перебрали все существующие альтернативы. На самом деле их
анализ находится все время в рамках формальной логики, в которой не принимаются
во внимание аргументы, связанные с физической (и философской!) сущностью
движения и с существованием законов природы. Претенциозное заключение Рейхенбаха: «Философская теория относительности, то есть
открытие дефинициального характера метрики во всех ее
деталях, справедлива независимо от опыта… Она составляет философское знание,
которое не может быть предметом критики со стороны отдельных наук» (там же,
с.197, 198) – выглядит просто смешно.
20. Формулировка
законов природы в физических теориях неявно содержит в себе и свойства
пространства-времени. Это хорошо показано в неоднократно упоминавшейся нами
книге А.А.Логунова. Однако только после Эйнштейна
стало ясно, что количественное описание свойств пространства
и времени дается законом преобразования координат при переходе от одной
инерциальной системы отсчета к другой. После этого отнюдь не тривиального
тезиса (который в терминах четырехмерного мира Минковского
сомкнулся с основной идеей Эрлангенской программы
Клейна) стало легко показать, что в законах классической механики неявно
содержатся преобразования Галилея, а в уравнениях Максвелла классической
электродинамики – преобразования Лоренца.
21. Эйнштейн А.
Сущность теории относительности. – М., 1955. – С.29. См. также: Эйнштейн
А. Собрание научных трудов. – М., 1966. – Т.2. – С.24. Ю.Б.Молчанов, приводя эту цитату в своей статье "О различных
смыслах отношения одновременности" (см.: Эйнштейновский сборник.
1968. – М., 1968), трактует ее в том смысле, что
«для СТО является существенным требование изучать свойства пространства и
времени, опираясь на реальные физические взаимодействия» (с.96), что СТО
требует «установления связи между разноместными событиями, т.е. наличия между
ними материальных взаимодействий» (с.94). По нашему мнению,
Эйнштейн подразумевает здесь нечто другое, а именно, связь, даваемую
соотношением (9). В нем речь идет вовсе не о взаимодействии, а всего
лишь о физическом определении понятия скорости любого процесса. Физическое
взаимодействие между объектами – это обмен энергией между ними. В
соотношении же (9) в лучшем случае можно видеть обмен информацией (о
показаниях линеек и часов) между точками х1
и х2.
22. Довольно часто можно
слышать мнение, что СТО есть не теория времени, а теория часов. Это совершенно
неверно. Под часами в теории относительности понимается символический
циферблат, показывающий то время, которое описывается законами СТО. Здесь
"часы" – это отнюдь не материальный механизм (или процесс). Ведь
его поведение кроме свойств времени определяется еще
законом функционирования указанного механизма во времени, а этот закон,
в свою очередь, управляется законами природы – механическими, квантовыми,
биологическими и т.д. в зависимости от того, какой процесс мы рассматриваем как
часы в обычном понимании. (Эти моменты хорошо прослежены в
статье Е.Л.Фейнберга "Можно ли рассматривать
релятивистское изменение масштабов длины и времени как результат действия
некоторых сил?" (Успехи физ. наук. – 1975. –
Т.116. – С.709–730.) Поэтому совершенно очевидны
ответы на часто задаваемые вопросы: как ведут себя "часы" при
ускоренном движении или при каких-либо внешних толчках? Ясно, что толчки никак
не влияют на нематериальный объект. При ускоренном же движении "часы"
будут показывать координатное время, соответствующее закону движения в
выбранной системе координат. Если бы "часы" были реальным механизмом,
то в процедуру синхронизации нужно было бы включить и сравнение скорости их
хода. В теории относительности (СТО и ОТО)
"скорость хода часов", или, что то же самое, "скорость течения
координатного времени t" (эти термины, конечно, нельзя
понимать буквально), задается коэффициентом при dt2 в
метрике. В системах координат, в которых записаны метрики (6) и (8), эти
коэффициенты постоянны. Значит, "часы идут с одинаковой скоростью" в
любой точке пространства и в любой момент времени – независимо от того,
какие материальные процессы там происходят (если они не искривляют пространство-время).
Это и есть свойство абсолютного пространства и времени Ньютона. Таким образом,
и в СТО сохраняется в силе понятие абсолютного пространства-времени, но только
если мы работаем в одной системе отсчета.
23. О тахионах см.: Корухов В.В. Теоретические и методологические
аспекты кинематики тахионов // Гуманитар. науки
в Сибири. – 1994. – №1. – С.25; Корухов В.В.,
Наберухин Ю.И. Сверхсветовые явления и
пространственно-временные отношения в тахионных
мирах // Философия науки. – 1995. – №1(1). – С.58.
24. Так оценивает
свой вклад Рейхенбах на с.166 книги «Философия
пространства и времени». Преувеличение значения собственных изысканий
характерно также и для книги Грюнбаума «Философские
проблемы пространства и времени», – см. хотя бы обвинение автором своих
оппонентов в "логической слепоте" (с.502).
Новосибирский государственный
университет
Naberukhin, Yu.I. Once more about synchronization of clocks in
the special theory of relativity
The original Einstein's method of deduction of the Lorentz
transformation given in his first article on the relativity theory is reproduced replacing the Einstein's rule for the clock
synchronization (1) with the generalized recipe (2) of Reichenbach.
It is found that a choice of values of ε ≠ ½ in the last is equivalent to the transition from the
ordinary rectangular Cartesian coordinate system to an oblique-angled
coordinate system in which the T axis is nonorthogonal
to the X axis. Such a generalization has
therefore no epistemological sense and entails neither conventionality of the
rules for clock synchronization nor conventionality of simultaneity. Standard
methods of deduction of the Lorentz transformation,
in contrast to Einstein's one, use no recipes of clock synchronization; they
are without mentions also in classical physics. The reason is that the clock
synchronization is introduced there implicitly, by the
velocity conception. Being in the single inertial frame
we can synchronize clock by any process, not necessary by light.