САМООРГАНИЗАЦИЯ, ЭНТРОПИЯ,
РАЗВИТИЕ: «ПОРЯДОК ИЗ ХАОСА» ИЛИ «ПОРЯДОК ИЗ АВТОНОМНОСТИ»?
Д.Г.Егоров
Междисциплинарное направление исследований, называемое
синергетикой, или теорией самоорганизации, сложилось при слиянии концепций
нескольких изначально независимых направлений: кибернетики, термодинамики
необратимых процессов, кинетической теории химических реакций, экологии,
физической теории фазовых переходов, фрактальной геометрии. Основа
синергетики – общность нелинейных процессов в системах самой
разнообразной природы (изучаемых как естественными, так и гуманитарными
науками), что позволяет описывать явления из самых разных областей с помощью
близких математических моделей. Явления самоорганизации имеют место в
физических, химических биологических, геологических и социальных системах, что
фиксируется в виде эмпирических фактов. Эти эмпирические факты теоретически
объясняются в рамках теории самоорганизации с помощью соответствующего
математического формализма – теории качественного анализа нелинейных
дифференциальных уравнений, которая имеет осмысленное
истолкование в рамках теоретической схемы, включающей в себя специфические
представления о системе, причинности, пространственно-временных отношениях,
связях с внешней средой [1]. Иными словами, в основе концепции самоорганизации
лежат философские принципы и представления, отличающиеся от оснований классического
естествознания.
Настоящая работа посвящена философскому анализу места
второго начала термодинамики в представлениях синергетики, в частности
критическому анализу представлений бельгийской школы И.Пригожина [2]. В рамках
этой школы развивается термодинамический подход к описанию самоорганизации: в
открытых системах, обменивающихся с окружающей средой потоками вещества или
энергии, однородное состояние равновесия может терять устойчивость и необратимо
переходить в неоднородное стационарное состояние, устойчивое относительно малых
возмущений. Эти стационарные состояния получили название диссипативных
структур. Явления самоорганизации в системах любой природы в рамках данных
представлений трактуются в термодинамических терминах, на основе понятия
энтропии. При этом, отталкиваясь от второго начала термодинамики и связанной с
ним проблемы соотношения обратимых и необратимых процессов в физике (из законов
механики вытекает постоянство энтропии, второй закон термодинамики требует ее
возрастания), представители бельгийской школы проводят грань между процессами
организации (механическими) и самоорганизации (термодинамическими, в которых
присутствует задаваемая ростом энтропии «стрела времени»).
Эти представления, по нашему мнению, дают основания для
критического анализа трактовки второго начала термодинамики. Речь здесь идет не
о физической его трактовке в рамках термодинамики (в пределах физики предмета
для спора нет), а о том, допустимо ли придание второму началу термодинамики
онтологического статуса, возможна ли его трактовка как общего принципа,
выходящего за рамки собственно термодинамики. Философская программа
И.Пригожина – это, по существу, расширенная трактовка термодинамики как
ключевой естественно-научной доктрины (из нее вытекают
эволюционное учение, представления о времени и т.д.).
С нашей же точки зрения, расширение термодинамического
подхода за пределы собственно термодинамики несет в себе внутреннее
противоречие, которое мы постараемся сейчас продемонстрировать. Заметим, что со
вторым началом термодинамики связаны даже не одна, а две проблемы: с одной
стороны, это проблема обратимости во времени уравнений механики, что вступает в
противоречие с термодинамической необратимостью процессов; с другой стороны,
второе начало термодинамики в его классическом истолковании противоречит также
идее прогрессивной эволюции. Как отмечает С.Д.Хайтун,
трудно сказать определенно, кто первый связал энтропию с беспорядком, но уже в
1883 г. Г.Гельмгольц как о само собой разумеющемся говорит об энтропии как
мере «дисорганизации» [3]. На наш взгляд, эти
проблемы взаимосвязаны и при этом в равной степени искусственны.
В одной из недавних работ Г.А.Мартынов пишет: «В начале века она (проблема противоречия между динамикой и
термодинамикой в связи с возрастанием энтропии. – Д.Е.)
привлекала к себе пристальное внимание; сейчас интерес к ней заметно упал, но
не потому, что проблема была решена, а скорее, потому, что все привыкли к
мысли, что ее решить невозможно. Я, однако, полагаю, что подобный пессимизм
вряд ли оправдан» [4]. Присоединяясь к этому высказыванию Г.А.Мартынова, мы, со
своей стороны, формулируем следующие утверждения. Обсуждаемое противоречие
существует в наших описаниях природы, а не в природе как таковой. Природа едина
по своей сути и не может обладать противоречащими друг другу свойствами [5].
Соответственно если мы имеем противоречивые описания природы, то по меньшей мере в одном из анализируемых описаний
содержится логическая ошибка либо оно неправомерно обобщено. Таким образом,
для того, чтобы решить означенную проблему, необходимо
не столько приложить методы математической физики, сколько провести тщательный эпистемологический анализ соотношения оснований механики и
термодинамики с целью нахождения этой скрытой ошибки, которая и приводит к
кажущемуся противоречию.
Такой эпистемологической ошибкой,
на наш взгляд, является придание второму началу термодинамики статуса всеобщего
закона. Закон – это утверждение, истинное всегда и везде, при любых
условиях. Что же касается второго начала термодинамики, то оно выведено на
вероятностных основаниях, и для любой системы существует пусть и крайне малая,
но не равная нулю вероятность его нарушения. «Противоречие» между динамикой и
термодинамикой – следствие этого неправомерного (для вероятностного по
своей сути утверждения) статуса второго начала, что и налагает запрет на некие
динамически возможные состояния. Запрет этот становится абсолютным (что и
создает логическое противоречие) фактом придания статуса закона вероятностному
по своей сути утверждению. Примером здесь может послужить следующая ситуация.
Проводится лотерея среди всех жителей Земли, в которой только один выигрыш.
Вероятность выигрыша столь мала, что каждый конкретный
человек принимает ее равной нулю. Таким образом, может возникнуть
«противоречие» между утверждениями, что шансов выиграть у
каждого конкретного человека нет, и тем, что кто-то обязательно должен выиграть.
Рассмотрим простую компьютерную модель
типа клеточного автомата, на которой традиционно демонстрируются статистические
закономерности термодинамических процессов. В данном случае будет проводиться
моделирование диффузии (см. рисунок). Позиция а
показывает начало процесса: на микроскопическом уровне (в модели это уровень
отдельных клеток, в природе – молекулы, броуновские частицы и т.д.) мы
имеем просто какое-то распределение параметров (X и не-Х)
в пространстве; общая картина существования капли вещества X во внешней
среде раскрывается только при макроскопическом взгляде на систему. Зададим
теперь алгоритм развития процесса: каждый временной квант какая-либо случайным
образом выбранная частица будет переходить в одну из пустых соседних клеток
(если они, конечно, в ее окружении есть). Через некоторое время картина,
представленная на рисунке позицией а, сменится картинами,
представленными позициями 6, в и т.д.
Это вполне соответствует реально протекающим процессам: капля чернил будет
растворяться в воде, а молекулы газа, собранные в одном месте, будут стремиться
заполнить весь объем.
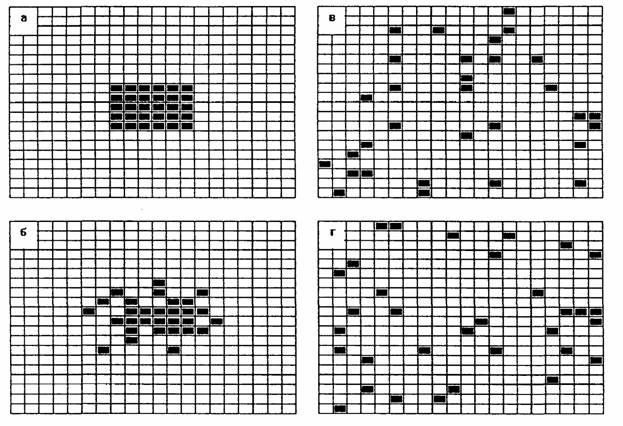
Компьютерное моделирование диффузии
Обратим внимание на то, что разница между системами,
показанными на рисунке позициями а и б–г, существует только на
макроскопическом уровне; с точки же зрения микроскопического описания мы имеем
просто другое распределение X в пространстве. Распределение,
представленное позицией а, принципиально не отличается от распределения,
представленного позицией г, и если мы сейчас
проделаем путь «а > б > в > г» в обратную
сторону, то мы снова получим распределение типа а. Почему, однако, мы не
наблюдаем подобных процессов в природе – скажем, концентрации рассеянной в
стакане воды капли чернил? Краткий ответ может быть таков: из-за недостаточного
времени наблюдения. Состояние а является
привилегированным только с точки зрения макроскопического описания, которое, в
свою очередь, существует только в чувственном восприятии наблюдателя, –
природа же состоит из атомов и энергетических полей. Переход из состояния 6
в состояние в или г – это столь же
редкое событие, как и переход из состояния 6 в состояние а, но
макроскопический наблюдатель не фиксирует разницы между состояниями б–г
(и огромным количеством других). Все эти распределения выступают под общим
именем "смесь" или "хаос" в отличие от "порядка" а.
Выделив в нашем численном эксперименте, условно говоря, из 10n
равновероятных состояний одно состояние а, мы, безусловно, увидим в
соответствии с теорией вероятности, что это уникальное состояние замещается
каким-то иным и очень долго не возникает вновь. В конце концов
оно все же возникнет – в течение 10n интервалов времени.
В теории тепловых процессов этой крайне низкой вероятностью
можно, конечно, пренебречь. На этом уровне описания термодинамика чрезвычайно
эффективна, так как позволяет заменять огромные динамические описания
несколькими макропеременными. Однако при анализе соотношения динамики и термодинамики
на уровне отдельных частиц, аппроксимируемых множествами с конечным количеством
элементов, даже исчезающе малая вероятность
возвращения системы в первоначальное состояние имеет принципиальное
значение – в том плане, что исчезает мистический запрет на какие-то
состояния динамической системы, с точки зрения термодинамики
имеющие меньшую энтропию. В вероятностных терминах утверждение второго закона
термодинамики о неуклонном росте энтропии лишается своей таинственности и
звучит почти как тавтология: более вероятные процессы происходят с большей
вероятностью. Поэтому введенное в 1928 г. Эддингтоном понятие "стрелы
времени" [6] представляется необоснованной экспансией термодинамики в
философию, – с тем же основанием можно ввести "стрелу
пространства", опираясь на тот факт, что тяготение на Земле всегда
направлено к ее центру.
Теперь обсудим другой аспект связанного со вторым началом
дуализма – противоречие с принципом эволюции. Это связано с трактовкой
второго начала как универсального закона, применимого к распределениям данных
любой природы. При таком подходе по распределениям каких-либо параметров по
известной формуле Шеннона (I = –∑pi In pi,
при условии ∑pi =1 [7]) рассчитываются значения
информации, а затем производится интерпретация в терминах роста-уменьшения
упорядоченности и т.д. [8]. Мы предпочитаем трактовать I как меру
разнообразия системы, а не степени ее упорядоченности, поскольку рассматривая
как энтропию значение I для какого-либо распределения данных,
исследователь фактически принимает гипотезу о том, что рассматриваемая им
совокупность объектов аналогична "молекулярному хаосу" идеального
газа Больцмана, т.е. эти объекты никак друг на друга не влияют.
Поясним этот тезис компьютерным экспериментом, аналогичным представленному на рисунке, но теперь в алгоритм сделаем
добавление: при встрече элементарные частицы будут взаимодействовать и
соединяться. С какого бы места б–г мы ни начали эксперимент, очень скоро
все частицы образуют единый кластер с min I, а стало быть, и энтропии,
если приравнивать данные понятия. Это, конечно, не опровержение второго начала
термодинамики (как принципа именно термодинамики), а просто иллюстрация
того, что ответ на вопрос о степени упорядоченности многих физических (не
говоря уже о социальных)
явлений (при использовании формулы Шеннона), как правило, формален или/и
бессмыслен: «...Распространенные представления о большей вероятности
равномерного распределения («хаоса») связаны с неправомерным распространением
гипотезы о равновероятности микросостояний за пределы
модели идеального газа» [9].
Аналогично эти представления сформулированы И.Л.Генкиным: «Обычно вероятности появления тех или иных
конфигураций подсчитываются на основе модели идеального газа. Но ясно, что
такая модель имеет весьма далекое отношение к мегамиру,
одна из основных черт которого – наличие дальне действующих сил
тяготения... Известно, что равномерное распределение вещества в пространстве не
может быть стационарным, а должно либо расширяться, либо сжиматься... вопреки
распространенным представлениям более вероятно именно состояние вещества с
развитой структурой, а отнюдь не первозданный хаос... Представление, согласно
которому появление предпочтительных структур маловероятно, основано на
недоразумении, на применении комбинаторики там, где она неприменима» [10].
Иначе говоря, «более вероятная структура (имеющая большую энтропию) может быть
как более развитой (сложной), так и менее развитой, в зависимости от конкретной
ситуации» [11]. Сложность как наличие структуры из подсистем и сложность как
термодинамическая вероятность – не одно и то же. Таким образом, проблема
противоречия второго начала термодинамики с принципом эволюции «оказалась
искусственной, и возникла она из-за непонимания природы понятия энтропии во
всей его глубине. Оказалось, что энтропия не может служить мерой сложности и
что эволюция в сторону усложнения вообще не противоречит эволюции в сторону
возрастания энтропии» [12].
Теперь рассмотрим вопрос, каким образом та или иная
трактовка второго начала термодинамики сказывается на представлениях о
развитии. Исходя из онтологического статуса второго начала
термодинамики И.Пригожин развивает философскую концепцию эволюции, в
основе которой лежит идея рождения порядка из хаоса [13]. Мерой порядка в
системе служит уменьшение в ней значения энтропии; последнее происходит за счет
увеличения энтропии (и беспорядка) в окружающей среде. Эволюция есть ряд
переходов «...хаос ® порядок ® хаос ® порядок...», регулируемых энтропийным принципом.
Мы не принимаем такой трактовки концепции развития. Прежде всего заметим, что для образования структур необходимым
условием является не поток энтропии, а поток энергии. Понятия энтропии и
энергии взаимосвязаны только для систем, соответствующих термодинамическим
идеализациям (где развитие действительно отвечает сценарию И.Пригожина). Однако
сводить к термодинамике все разнообразие системообразующих
мотивов, как показано выше, недопустимо: мир не есть огромный резервуар,
наполненный идеальным газом (в котором все связи и взаимодействия качественно
равноценны). Напрашивающийся, хотя отнюдь не
единственный, контрпример здесь – развитие жизни
на Земле. Источник энергии, за счет которого на планете происходит
последовательное увеличение как количества, так и
качества биомассы, – солнечный свет. При этом излучение Солнца не
сопровождается увеличением хаотизации его структуры, – она, скорее,
напротив, усложняется в результате термоядерных реакций, побочным результатом
которых и является солнечный свет. Действительно, порядок и хаос в процессе
развития оказываются сопряженными – в пространстве и/или во времени [14].
Здесь, однако, уместно вспомнить утверждение Юма о том, что
пространственно-временная сопряженность не есть доказательство причинной связи.
День и ночь тоже сопряжены во времени, но день рождается не из ночи, а в
результате увеличения освещенности поверхности в процессе вращения Земли.
Таким образом, схему «...хаос → порядок → хаос →
порядок...» мы заменяем на схему «...порядок ± хаос –
порядок ± хаос – порядок...» [15]. Наши представления здесь соответствуют
идеям многих других авторов. Так, Ю.В.Сачков пишет, что «любой эволюционный
процесс берет свое начало не с хаотического состояния, а является порождением
других эволюционных процессов» [16]. Он также подчеркивает связь представлений
о хаосе как первопотенции бытия и онтологических
воззрений на второе начало термодинамики: «...Представления о хаосе
поддерживались и питались "выводами" о неизбежности тепловой смерти
Вселенной... Подобные представления о хаосе как о некотором исходном и основном
состоянии материи в литературе получили оценку как один из мифов прошлого, еще
владеющих мышлением современного человека" [17].
С.Вир указывает составляющие элементы убеждений, касающихся
хаоса: 1) изначальное состояние природы хаотично; 2) порядок есть
нечто, вносимое в хаос, навязываемая ему структура; 3) внутри этой
структуры заключен скрытый хаос второго порядка; 4) как только энергия,
поддерживающая порядок, перестает поступать, все вновь возвращается к хаосу
[18]. В наше время эти убеждения подпитываются онтологизацией
второго начала термодинамики, однако в историческом плане они имеют длительную
традицию, восходя по меньшей мере к поэме Гесиода
«Теогония»: «В самом начале был сотворен Хаос, а потом широкогрудая Земля...»
[19]. Вместе с тем существует и другая философская традиция имманентности
организации, которая, как отмечает С.Бир,
восходит к Св.Иоанну. «Вначале было Слово» (Иоанн,
1:1) – в этом изречении утверждается атрибутивность процессов организации
в природе. «...Решение интересующей нас проблемы, – пишет С.Бир, – которое можно извлечь из рассмотрения
новейших научных идей, сводится к следующему. Мы вполне можем исходить из нехаоса; и нам не нужна некая «вещь», заключающая в
себя «принцип» имманентности организации. Единственно, что нам нужно, –
это язык, отличный от языка Гесиода...» [20]. Под языком здесь, по нашему
мнению, подразумевается парадигма.
Действительно, если мы непредвзято рассмотрим естественно-научные факты, то обнаружим, что порядок гораздо
более распространен, нежели хаос. Все живые существа суть упорядоченные
структуры. Земля сложена кристаллическими породами, т.е. также структурноупорядоченными веществами. Планетные системы
построены отнюдь не хаотично, и звезды объединены в скопления и далее в
галактики, имеющие, как правило, четкую спиралевидную структуру. Таким образом,
Вселенная в целом предстает как упорядоченная структура, в которой наблюдаются
вкрапления хаотических фрагментов (на том или ином уровне). «Порядок более
естественен, чем хаос, – утверждает С.Бир, –
...Придя [к этой мысли], я порвал с описательными постулатами Гесиода,
давившими на мое сознание грузом почти трехтысячелетней
давности. Это утверждение позволило мне совершенно по-новому взглянуть на
системы" [21].
Конструктивный момент в концепции И.Пригожина – это,
на наш взгляд, указание на роль случайности в эволюции диссипативных систем.
Случайность, однако, опирается не на отсутствие порядка (это лишь частный
случай проявления случайности), а на независимость элементов системы [22].
Но если не хаос, то тогда что выступает основанием для
проявления развития в эволюции систем? Мы считаем, что таким основанием служит
активность, или автономность, элементов системы, т.е. относительная независимость
поведения систем от их внешнего окружения. Это более сложный феномен, чем
независимость. "Независимость, пишет Ю.В.Сачков, – конечно, является
существенным признаком автономности, но далеко не самым интересным и, скажем,
не определяющим. Адекватная трактовка автономности вырастает на базе познания
живых систем... Автономность объектов и систем есть
прежде всего их действие по внутренним побуждениям, по законам функционирования
своей внутренней организации. Соответственно этому строится и система базовых понятий,
выражающих идею автономности. При характеристике автономных, живых систем
первостепенное внимание уделяется проблеме внутренней активности при их
функционировании..." [23]. По нашему мнению, автономность элементов лежит
в основе самоорганизующихся процессов не только в живых, но и в неорганических
системах. Конечно, абсолютно независимые сущности не создадут никакой
структуры, – «образование структуры из некоторых элементов можно
рассматривать как ограничение независимости последних» [24]. Структура, таким
образом, есть результат взаимодействия независимости и зависимости.
Что вообще есть «хаос»? Это понятие «характеризует
прежде всего структуру таких систем, где элементы внутренне динамичны, но их
поведение ни в малейшей степени не согласуется, не коррелирует
друг с другом, и отсутствуют обратные связи» [25]. Прообраз этих систем –
идеальный газ [26]. В таких системах при любом увеличении их размеров и степени
хаотичности распределений элементов процессы самоорганизации невозможны.
Необходимое условие для реализации процессов самоорганизации – способность
элементов системы вступать как минимум в два качественно различных типа
взаимодействия.
Рассмотрим в связи с этим общепринятое обобщенное
математическое описание синергетических систем. Как правило,
таким описанием является система нелинейных параболических уравнений типа
реакция – диффузия: dU/dt=F(U)+DΔU, где U –
вектор состояния элементарного объема возбудимой среды (для химической системы
компоненты вектора состояния – это концентрации реагентов, для
экологической – количество животных на единицу площади и т.д.); матрица D
определяет коэффициенты переноса (вещества, энергии, информации);
нелинейная функция F(U) задает скорость взаимодействия
(химических реакций, конкуренции за питание, энергию и т.д.) в элементарном
объеме [27]. При отсутствии этих минимальных условий (наличия обмена веществом,
и/или энергией, и/или информацией, а также каких-либо нелинейных [28]
преобразований элементов) никакая самоорганизация не произойдет при любом уровне
хаоса и при любом размере системы. И напротив, если эти условия
соблюдены, процессы самоорганизации могут начаться, причем безотносительно
того, каким было начальное состояние системы: хаотическим или же как-то
изначально упорядоченным. Таким образом, на физическом уровне активность может
выражаться в виде способности элементарных частиц к проявлению нескольких типов
взаимодействий (например, притяжения и отталкивания); на уровне химических
взаимодействий активность проявляется в способности атомов принимать различные
формы валентности; биологические системы характеризуются еще большей
вариативностью поведения элементарных компонентов систем и т.д. Зависимость
выступает здесь в форме внешнего воздействия на систему [29], – в системе
уравнений это выражается заданием граничных условий. Математически процессы
самоорганизации фиксируются при решении уравнений указанного типа в виде
стационарных решений, когда аргумент не зависит от времени, либо в виде
решений, зависящих от времени, но не зависящих от координаты (пространственные
и временные диссипативные структуры соответственно).
Поэтому в идеальном газе никакая
самоорганизация не возникает ни при каком увеличении
количества элементов системы, нагрева и т.д. Простейшие процессы
самоорганизации может демонстрировать совокупность твердых частиц, могущих
сцепляться между собой и реагировать упруго, в поле тяжести: при насыпании кучи частиц в какой-то момент времени сходит
лавина, после чего процесс повторяется (так называемая самоорганизованная
критичность [30]). Этот простейший процесс самоорганизации имеет и простейший
аттрактор в фазовом пространстве – притягивающий фокус. Более вариабельную
автономность демонстрируют химические ионы, способные
принимать различные валентные состояния, что соответственно увеличивает сложность
процессов самоорганизации, могущих идти в таких системах. При этом, по нашему мнению, нельзя утверждать, что порядок в
реакциях типа реакции Белоусова – Жапотинского и
аналогичных им "обеспечен" молекулярным хаосом раствора (т.е. хаосом
на более низком структурном уровне), ибо для их протекания совершенно
безразлично, движутся ли ионы в растворе хаотично или имеют предпочтительные
направления движения; главное – это их способность к автокатализу,
обеспечиваемая мультивалентностью, т.е. автономностью
их поведения.
При этом обнаруживаются более сложные аттракторы в фазовом
пространстве решений – предельные циклы, торы и странные аттракторы. При
возникновении странного аттрактора система ведет себя с точки зрения случайного
наблюдателя хаотично, но это детерминированный хаос [31], который по-прежнему
описывается той же базовой системой уравнений. Точное предсказание поведения
системы тогда в реальности становится невозможным и может быть описано только в
вероятностных терминах. Тем не менее детерминированный
хаос отличается от собственно хаоса своими динамическими характеристиками и
может рассматриваться как вариант порядка (так как структурные связи элементов
при нем не разрушаются) [32]. Может быть, имеет смысл говорить о взаимосвязи
хаоса с порядком в том аспекте, что такого рода детерминированный хаос может
быть источником флуктуации (генератором случайности), которые затем перерастают
в последующие процессы самоорганизации. Однако, по нашему мнению, первоосновой
развития является именно автономность, ибо в конечном
счете стохастичность (вероятностный детерминизм) оказывается как формой
выражения, так и следствием самоорганизации.
Безусловно, автономность опирается на вероятность, –
без вероятностного детерминизма автономность вообще немыслима (если элемент
имеет изначально заданную реакцию, то о какой автономности может идти речь?).
Однако "если первоначально вероятность соотносилась с хаотическими
состояниями систем, то ныне она оказывается встроенной
в общее учение о сложных системах: ее природа связана с раскрытием внутренней
динамики систем и ее направленности" [33]. Иными словами, мы разделяем
точку зрения Ю.В.Сачкова об онтологическом статусе случайности как элементе
бытия, лежащем в его основании ("самостоятельное начало мира" [34]).
Случайность может быть следствием собственно хаоса, а может быть закономерным
результатом развития системы (как показывают математические исследования,
"детерминированный хаос", или вероятностный порядок, возможен уже в
системе из трех тел).
Как соотносятся представления о развитии, формулируемые в
рамках теории самоорганизации, с философской трактовкой развития, в частности,
предлагаемой в диалектической теории развития? По нашему
мнению, на философском уровне концепция самоорганизации не есть какая-то новая
теория развития: она не отменяет и даже не изменяет таких философских принципов
развития, как переход количественных изменений в качественные, единство и
борьба противоположностей и отрицание отрицания, – она им соответствует.
Вновь обращаясь к анализу математических форм выражения концепции
самоорганизации (см. уравнение выше), заметим, что по
крайней мере два этих принципа имеют ясное математическое обоснование: принцип
перехода количественных изменений в качественные описывает бифуркационные
переходы, когда при плавном увеличении какого-либо параметра происходит
качественная перестройка поведения системы (ветвление решений); принцип
единства и борьбы противоположностей отражает то свойство сложных систем, что
без наличия как минимум двух качественно различных типов взаимодействий
(отображаемых в двух членах анализируемой формулы) никакая самоорганизация и,
следовательно, никакое развитие не произойдет. Это основание для развития на
основе четырех фундаментальных физических взаимодействий (слабого, сильного,
электромагнитного и гравитационного) различных типов физических, а затем
химических, биологических и других процессов – как синтеза минимум двух
качественно различных взаимодействий. Так, в отсутствие гравитационного поля (выполняющего роль источника переноса) только лишь на основе
электромагнитного взаимодействия никакие химические и биологические системы в
принципе не могут возникнуть.
Совместное рассмотрение автономности и иерархичности
открывает нам еще более интересный феномен: мы обнаруживаем системы, элементы
которых тоже являются самоорганизующимися системами, эволюция этих последних
приводит к их изменению, что влечет за собой изменение стиля эволюции
макросистем, т.е. эволюцию эволюции. Эта проблема в явном виде впервые была
поставлена А.Шеллом [35] и активно дискутируется в последние десятилетия [36],
хотя до создания ясной теории здесь еще достаточно далеко.
В заключение сформулируем следующие выводы. Онтологическая
трактовка второго начала термодинамики, на наш взгляд, не является правомерной.
Ее результат – ложные «противоречия» между термодинамикой, с одной
стороны, и механикой и теорией развития – с другой. В основе самоорганизации, по нашему мнению, лежит автономность
(активность) элементов системы, а в основе автономности – случайность
(стохастичность, вероятность), что, однако, не тождественно хаосу.
Примечания
1. См.: Крон В., Кюпперс Г., Паслак Р. Самоорганизация: генезис научной
революции // Концепция самоорганизации в исторической
ретроспективе. – М., 1994. – С.86–103; Степин B.C.
Теоретическое знание. – М., 2000; Егоров Д.Г. Смена парадигм в
современных науках о Земле. – Мурманск, 2001.
2. См.: Николис Г.,
Пригожин И. Самоорганизация в неравновесных системах. – М., 1979; Они
же. Познание сложного: Введение. – М., 1990;
Пригожин И.Р., Стенгерс И. Время, хаос и
квант: К решению парадокса времени. – М., 1999.
3. Хайтун С.Д.
Развитие естественно-научных взглядов о соотношении
закона возрастания энтропии и эволюции // Концепция самоорганизации в
исторической ретроспективе. – М., 1987. – С.165.
4. Мартынов Г.А. Неравновесная статистическая
механика, уравнения переноса и второе начало термодинамики // Успехи
физических наук. – 1996. – Т. 166, № 10. – С.1121.
5. Противоречивыми могут быть наши описания ее отдельных
сторон, которые могут обладать противоположными, но никак не противоречащими
друг другу свойствами.
6. См.: Eddington A. The nature of the physical world. –
Ann Arbor, 1958.
7. См.: Шеннон К. Работы по теории информации и
кибернетике. – М., 1963.
8. См.: Климонтович Ю.Л. Проблемы статистической
теории открытых систем: критерии относительной степени упорядоченности
состояний в процессе самоорганизации // Успехи физических наук. –
1989. – Т. 158. – С.59–92; Войтеховский Ю.Л.
Симметрия и структура эволюционирующей системы – к анализу соотношения инвариантов:
К структурной теории сложных минеральных ансамблей. I, II // Синергетика
геологических систем. – Иркутск, 1992. – С.10–15; и др.
9. Хайтун С.Д.
Развитие естественно-научных взглядов… – С.183.
10. Генкин И.Л.
Энтропия и эволюция Вселенной // Астрономия, методология,
мировоззрение. – М., 1979. – С.181, 182.
11. Хайтун С.Д.
Развитие естественно-научных взглядов… – С.182.
12. Там же. – С.186.
13. См.: Пригожин И.Р., Стенгерс И. Время, хаос и квант…
14. Эта сопряженность тривиально следует из закона исключенного третьего: если все состояния системы мы дихотомически делим на «хаос» и «порядок», то интервалы порядка не могут быть разделены ничем, кроме хаоса.
15. Знак ± означает, что хаос не обязательно разделяет два различных режима упорядоченности.
16. Сачков Ю.В. Вероятностная революция в
науке. – М., 1999. – С.78.
17. Там же. – С.77.
18. См.: Бир С.
Кибернетика и управление производством. – М., 1965. – С.277.
19. Цит. по: Бир С.
Кибернетика и управление производством. – М., 1965. – С.279.
20. Бир С.
Кибернетика и управление производством. – М., 1965. – С.283.
21. Там же. – С.285.
22. "Независимость лежит в основе случайности..." (Сачков Ю.В. Вероятностная революция в науке. – С.78).
23. Сачков Ю.В. Вероятностная революция в
науке. – С.109.
24. Там же. – С.81.
25. Там же. – С.76.
26. «...само слово «хаос» происходит из того же корня, что и слово «газ»» (Сачков Ю.В. Вероятностная революция в науке. – С.76).
27. См.: Давыдов В.А., Морозов В.Г. Галилеевы преобразования и распространение автоволновых фронтов во внешних полях // Успехи
физических наук. – 1996. – Т. 166, № 3. – С.327.
28. Так, для химических систем условием дальнодействия выступает «автокатализ» (А + 2Х → ЗХ) и/или «перекрестный катализ» (А + X → 2У; В + У → 2Х); для систем иной природы требуются другие нелинейные эффекты, имеющие, однако, аналогичное математическое выражение (см.: Пригожин И.С., Стенгерс И. Время, хаос, квант. – С.65).
29. В отличие от организации, где каждое действие над всеми элементами системы предписано извне, в случае самоорганизации это воздействие является неспецифическим.
30. См.: Bak P., Tang C., Winsenfeld
K. Self-organized criticality // Phys. Rev. A. – 1988. – V. 38. – P.364–375.
31. По нашему мнению, термин «детерминированный хаос» не слишком удачен, так как лексически близок к представлению о хаосе. В сущности же речь идет о вероятностном порядке, который имеет с хаосом общее свойство – вероятностные распределения значений параметров (стохастичность), но совершенно отличается от него наличием структуры.
32. Что выражается на уровне качественного анализа уравнений в
том, что фазовая область фрактальных траекторий может быть определена.
33. Сачков Ю.В. Вероятностная революция в науке. – С.119.
34. Сачков Ю.В. Случайность формообразующая //
Самоорганизация и наука: опыт философского осмысления. – М., 1994. –
С.132.
35. См.: Shull A.
Evolution. – L., 1936.
36. См.: Завадский К.М., Колчинский
Э.И. Эволюция эволюции. – Л., 1977; Методология исследования
развития сложных систем: естественно-научный
подход. – Л., 1979. – С.294, 295; Бранский В.П.
Теоретические основания социальной синергетики // Вопросы
философии. – 2000. – № 4. – С.112–129; и др.
Кольский НЦ РАН,
г. Апатиты Мурманской
обл.
Yegorov D.G.
Self-organization, entropy, development: «order from chaos» or «order from
autonomy»?
There is the
philosophy analysis of the second thermodynamics low on the sinergetics?
in special – the critical analysis of the second
low ontology interpretation from the I.Prigogine. The
relations between the second thermodynamics low and mechanics- evolution conseptions is discussed. In
opposite to the belgian sinergetics school evolution conception there is the
concept concerning the autonomy as the basis of the self-organization, and the probobality (but not chaos) is the basis of the autonomy.