Первый кризис оснований математики и пифагорейская философия

Е.Н.Камельчук

Отправным пунктом всех является удивление, что дело должно обстоять именно так… кажется удивительным… что могло бы быть нечто такое, чего нельзя было бы измерить даже самой маленькой общей мерой.

Аристотель (Мет. 983а)

Введение

Исследование, проводимое в рамках данной статьи, является междисциплинарным, оно выполнено на стыке истории науки, философии науки и истории философии. Мы начнем его со следующего, пусть несколько спорного, утверждения: античная математика, даже став вполне самостоятельной и независимой от философии наукой (чего не удалось сделать, например, физике или биологии), сохранила, тем не менее, теснейшую связь с философией, и даже более того – с конкретной философской школой. Несколько огрубляя, можно сказать, что античная математика была пифагорейской математикой. По крайней мере, именно ордену пифагорейцев принадлежат первые выдающиеся достижения в этой науке и именно с ним, так или иначе, было связано все дальнейшее ее развитие [1]. Такое состояние дел имело, несомненно, свои плюсы: ясно, например, что для успешного развития науки весьма важно существование некоторой корпорации представителей данной науки и ее преподавателей. Пифагорейское “товарищество” [2] как раз и выполняло, до известной степени, роль социального института, являющегося “законодателем мод” в математике и облегчающего общение ее представителей между собой.

Что же касается сложностей, проистекающих из данной ситуации, то их можно разделить на две группы, которые, впрочем, тесно взамосвязаны. Первая сложность заключается в том, что пифагорейский орден был довольно-таки замкнутой, так сказать, “герметичной” организацией. Пифагорейцы, как известно, отнюдь не горели желанием делиться “эзотерическими” результатами своих, в том числе и чисто математических, изысканий с “профанами”, не состоявшими в ордене, – вспомним о сооружении ими “вредоносной могилы” для Гиппаса, разгласившего секрет какого-то пифагорейского достижения (то ли это было доказательство существования иррациональных чисел, то ли способ построения додекаэдра) [3]. Более того, доказательства сообщались даже не всем членам гетерии. Так, “акусматики”, т.е. “новоначальные” члены ордена, или “послушники”, узнавали лишь формулировки некоторых результатов, но не знали стоявших за этими формулировками дедуктивных процедур [4]. Поэтому хотя пифагорейцы и повлияли, вне всяких сомнений, на написание “Элементов” Евклида, но сами они такого рода книг не писали, – их книги, судя по цитатам (часто предположительным), приводимым античными авторами, были довольно-таки “непрозрачны” для посторонних читателей. Далее в статье мы будем рассматривать именно такой “герметический” отрывок из Теона Смирнского, имеющий явно пифагорейское происхождение. Читая некоторые “пифагорейские” места у Теона или, скажем, у Прокла, невозможно отделаться от ощущения, что автор то ли не понимает всей сути приводимых результатов, то ли не желает своего понимания показывать. Поэтому историк науки или историк философии не располагает достаточной информацией о многих важных аспектах пифагорейской математики и, как следствие, о важнейших моментах первого кризиса оснований математики. Так, мы, строго говоря, не знаем о том, как именно возник или проявился данный кризис и как конкретно он был разрешен. Предположения и реконструкции, имеющиеся в нашей статье, являются, следовательно, неизбежными.

Вторая сложность, о которой нужно упомянуть, состоит в том, что пифагорейская математика была “служанкой” пифагорейского учения и его важнейшей опорой. Это означает, в частности, что если какой-нибудь математически бесспорный результат оказывался для пифагореизма “неудобным” философски, то ему нужно было придать такой вид или проинтерпретировать таким образом, чтобы он не противоречил философским догмам, а лучше всего подтверждал их. Именно так, с нашей точки зрения, обстоит дело с первым кризисом математики. Его чисто математическое разрешение, т.е. обнаружение иррациональных чисел, подрывало фундаментальный пифагорейский тезис “единица – начало всего” [5], носивший не только математический, но и мистико-философский характер. Можно не сомневаться, что пифагорейцы делали все возможное, ища достойный (разумеется, с их точки зрения) выход из этого положения, и есть все основания утверждать, что они его нашли.

Учитывая сказанное выше, сформулируем теперь наши задачи. Следует, во-первых, обнажить суть первого кризиса основ математики. Во-вторых, нужно, пусть даже на уровне предположений (впрочем, вполне убедительных), указать способ, с помощью которого математики античности преодолели данный кризис [6]. В-третьих, – и это центральная задача статьи, – надо продемонстрировать тот факт, что пифагорейцам удалось справиться с “кризисом основ” их философии, возникшим вследствие успешного разрешения математического кризиса. Отметим, что уже сама постановка такой задачи говорит о научной новизне статьи, и думается, что небезынтересным будет и предлагаемое ее решение.

Первый кризис основ математики

Говоря современным языком, первый кризис основ математики возникает при сопоставлении двух следующих результатов:

(*1) ([p, q Î Z) (p² ¹ 2q² ), т.е. уравнение p² = 2q² не имеет решения в целых числах;

(*2) если S и D суть числа, выражающие длину соответственно катета и гипотенузы равнобедренного прямоугольного треугольника, то D² = 2S² (частный случай теоремы Пифагора).

Трудно сказать, в какой именно последовательности античными математиками была установлена истинность этих положений, – думается, именно в той, в которой они приведены нами [7]. Мы, кроме того, считаем, что оба этих результата были получены самим Пифагором, – по крайней мере, в этом нет ничего невозможного [8]. Конечно, первое положение было сформулировано им на совершенно другом математическом языке. Для достижения наших целей удобнее работать именно со “старой” формулировкой.

Предложение (*1) на языке античной математики звучало так:

(*1а) не существует квадрата, равного двойному квадрату.

Но ведь простейший частный случай теоремы Пифагора как раз и говорит о том, что (*1а) неверно: площадь квадрата, построенного на диагонали квадрата, равна удвоенной площади квадрата исходного. Заметим, кстати, что для доказательства (*2) совсем не обязательно знать общую формулировку теоремы Пифагора, – чтобы убедиться в истинности этого положения, достаточно просто взглянуть на любой из чертежей, представленных на рис. 1 и 2.

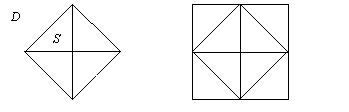
Рис. 1 Рис. 2

Ясно, что площадь квадрата со стороной D вдвое больше площади квадрата со стороной S.

Теперь вернемся к (*1а). Как явствует из истинного суждения (*1), положение (*1а) действительно верно в виде

(*1b) не существует такого двойного квадрата, сторона которого соизмерима со стороной исходного квадрата [9].

Истинность положения (*1b) доказывается очень простым и изящным рассуждением, автором которого был, полагаем, Пифагор и суть которого сводится к следующему: допустив ложность (*1b), мы допускаем существование числа, являющегося одновременно четным и нечетным, что абсурдно [10]. Осознание разницы между (*1а) и (*1b) вплотную приближает нас к пониманию кризиса античной математики.

Вспомним вынесенную в эпиграф цитату из “Метафизики” Аристотеля об “удивительности” существования несоизмеримых отрезков. Действительно, для обыденного сознания, не осуществляющего тщательной рефлексии над собственным содержанием, кажется очевидным, что

(АС) любые два отрезка соизмеримы, –

мы называем это положение Аксиомой Соизмеримости [11]. Учитывая же то обстоятельство, что до построения аксиоматических теорий (в которых каждая аксиома задается явно и ее наличие тем самым четко осознается) было еще весьма далеко, мы должны понимать, что (АС) воспринималась первыми математиками настолько сама собой разумеющейся, что различие между (*1а) и (*1b) совершенно не могло быть осознано. Более того, положение (*1b) не могло быть даже просто записано! Но в таком случае верное положение (*1) должно было восприниматься древними именно в виде ложного суждения (*1а), которое, само собой, находится в противоречии с теоремой Пифагора или ее частным случаем, очевидным из чертежей на рис. 1 и 2.

Излагая сказанное выше более современным языком, можно констатировать, что рассуждения о невозможности двойного квадрата, неявно опираясь на (АС), справедливы лишь в поле рациональных чисел Q, а геометрические результаты (в том числе и теорема Пифагора), основанные на столь же интуитивном представлении о непрерывности (= континуальности), справедливы в более широком поле действительных чисел R [12]. Мы полагаем, что именно появление теоремы Пифагора, столь привычной для нас со школьной скамьи, стало парадоксом перед лицом очевиднейшего рассуждения о невозможности двойного квадрата, основанного на неявно подразумеваемой (АС). Сейчас ясно, что этот кризис оснований был этапом, необходимым для выхода математики из состояния преднауки и прогресса теоретического мышления, но это не должно затушевывать серьезности кризиса: шок был чрезвычайно велик [13].

Перед тем как мы перейдем к следующему разделу, полезно обсудить два момента. Первый из них является ответом на возможное возражение: что, дескать, теорема Пифагора была известна задолго до своего номинального автора (“вавилонянам еще за тысячелетия до него были известны свойства прямоугольных треугольников” [14]), – но это почему-то не приводило ни к каким кризисам. С одной стороны, это верно. Действительно, вавилоняне умели приближенно вычислять длину диагонали квадрата с большой точностью, – до нас дошли вавилонские таблицы так называемых “пифагоровых троек” [15]. Но с другой стороны, первый кризис возникает из сопоставления теоремы Пифагора с предложением о невозможности двойного квадрата, а последнее опирается на теорию делимости, существование которой, как указывает А.П.Юшкевич, “в вавилонской математике ничем не засвидетельствовано” [16].

Второй момент, который для нас гораздо более важен, касается как раз положения о невозможности существования двойного квадрата. Справедливость данного положения устанавливается, как мы уже указывали, простым рассуждением, которое тот же А.П.Юшкевич называет “арифметическим доказательством иррациональности” [17], т.е. несоизмеримости. За процитированным выражением просматривается такой, вполне “традиционный”, ход мысли: поскольку предположение, что диагональ исходного квадрата (= сторона двойного) рациональна (= соизмерима со стороной исходного), приводит к абсурду, постольку она иррациональна (= несоизмерима со стороной исходного). Конечно, такой ход мысли возможен, – например, в голове современного школьника, но он совершенно невероятен применительно к мышлению античного математика! Ведь для этого нужно, выписав (АС) явно, предполагать, что могут в принципе существовать несоизмеримые отрезки. Такое рассуждение было бы sui generis “теоремой чистого существования” иррациональных чисел. Зная, что не всякий даже современный математик (например, конструктивист) одобрил бы такого рода “чисто абстрактные” рассуждения, можно ли предполагать, что древние удовлетворились бы ими?! Нет, это совершенно невероятно! Неясно, кроме того, в чем мог бы здесь заключаться какой-либо кризис и почему в таком случае ранние пифагорейские математики назвали бы диагональ квадрата “неприличной”. Словом, мы полагаем, что для античного математика рассуждения, удостоверяющие невозможность существования двойного квадрата, могли лишь подчеркивать парадоксальность и “кризисность” ситуации, а выход из кризиса мог заключаться в прямом, наглядном и “конструктивистском” доказательстве несоизмеримости стороны и диагонали квадрата. Неясно, кроме того, как может Эвдем утверждать, что “Пифагор… открыл теорию несоизмеримых” [18], если тот дал всего лишь такое вот “абстрактное” доказательство наличия несоизмеримости. Как пишет М.Е. Паев, “к осознанию значения невозможности решения в целых числах уравнения p² = 2q² могло привести только открытие явления несоизмеримости прямым наглядным путем” [19]. Гипотетической реконструкции такого “прямого наглядного пути” и посвящен следующий раздел.

Преодоление кризиса

Зададим себе вопрос: что бы мы стали делать, если бы оказались в описанной ситуации? У нас есть два совершенно простых и ясных рассуждения, которые, по всей видимости, противоречат друг другу. Мы не отдаем себе отчета в том, что неявно подразумеваемая (АС) не работает в области наших геометрических представлений, но знаем, что диагональ квадрата является каким-то “неприличным” отрезком, – тот факт, что она является стороной “невозможного” двойного квадрата, вроде бы свидетельствует о существовании неких странных четно-нечетных чисел. (Возможно, что именно эти размышления отражаются в следующем свидетельстве Стобея: “число имеет два особых вида: четный и нечетный, и третий, смешанный из обоих – четнонечетный” [20]). Интересно было бы посмотреть на такие числа! Сделать это, по всей видимости, довольно просто, – нужно лишь соизмерить сторону и диагональ квадрата, т.е. найти некий отрезок, который укладывался бы целое число раз как в стороне, так и в диагонали. Вот тогда-то мы и узнаем, на какое четно-нечетное количество (= q) равных отрезков следует разделить сторону квадрата, чтобы, взяв этот отрезок опять-таки четно-нечетное число раз (= p), получить квадрат диагонали.

Теперь перед нами стоит другой вопрос: как же древние соизмеряли отрезки? Ответ на него, думаем, весьма прост: они делали это с помощью так называемого “алгоритма Евклида” [21]. Говоря современным языком, для того чтобы соизмерить отрезки α и β (положим, для определенности, что α > β), нам нужно найти некоторый набор чисел (N_i и R_i) [22], позволяющий записать следующую совокупность равенств:

(АЕ₀) α = N₀β + R₀;

(АЕ₁) β = N ₁R₀+ R ₁;

(АЕ₂) R₀ = N ₂ R ₁ + R ₂;

…

(АЕ_i) R_{(i – 2)} = N _i R _{(i – 1)} + R _i;

…

(АЕ_K) R_{(K – 2)} = N _K R _{(K – 1)} + R _K;

(АЕ_{(K + 1)}) R_{(K – 1)} = N _{(K + 1)} R _K.

Очевидно, что когда процесс прервется на каком-то (у нас на (К + 1)‑м) шаге [23], величина R_K будет соответствовать длине отрезка γ, соизмеряющего α и β [24]. Используя эти равенства “в обратном порядке”, т.е. подставляя (АЕ_{(K + 1)}) в (АЕ_K), (АЕ_K) в (АЕ_{(K - 1)}) и т.д., мы получим в конце концов выражения α = pγ и β = qγ, где p и q будут какими-то алгебраическими комбинациями чисел из набора N_i.

Не следует, заметим сразу, думать, будто бы алгоритм Евклида является какой-то хитрой и “заумной” процедурой. Совсем напротив, в нем описывается последовательность действий, которую выполнил бы всякий смекалистый человек, если бы перед ним стояла соответствующая чисто практическая задача на соизмеримость отрезков, скажем требовалось бы разделить на равные кусочки два прутка золота. Действительно, если меньший отрезок (= пруток) β не укладывается в больший отрезок α целое число раз, то мы станем искать отрезок R₀, являющийся “остатком” от “деления” α на β, как показано на рис. 3.

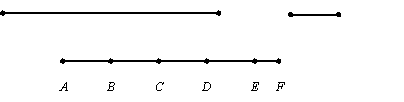
Рис. 3

На этом рисунке AF = α, AB = BC = CD = DE = β, а отрезок EF является “остатком” и соответствует величине R₀ в записаном выше алгоритме Евклида. Собственно говоря, рис. 3 является иллюстрацией частного случая формулы (АЕ₀), где N₀ = 4. Если окажется, что EF укладывается в отрезке β целое число раз (скажем, три раза), то процедура закончена: EF и будет “соизмеряющим” отрезком, тогда в (АЕ₁) множитель N₁ = 3, а величина R₁ = 0. Если же окажется, что EF не укладывается в отрезке β целое число раз, тогда нам следует искать отрезок, соизмеряющий EF и β, поскольку очевидно, что такой отрезок будет соизмеряющим также и для отрезков α и β. Мы должны, следовательно, найти отрезок R₁, являющийся “остатком” от “деления” β на EF, или, иначе говоря, осуществить второй шаг алгоритма, соответствующий (АЕ₁). Затем мы должны установить, укладывается ли R₁ в EF целое число раз… и т.д. и т.п.

Теперь представим себе, что некие древние математики, скажем Пифагор “со товарищи”, стали осуществлять описанную выше процедуру, “алгоритм Евклида”, для отрезков D и S, являющихся соответственно диагональю и стороной квадрата. Как мы сейчас понимаем, в этом случае процесс должен длиться бесконечно, т.е. не может иметь какого-то последнего (K + 1)‑го шага, на котором остаток R_K целое число раз уложился бы в остаток R_{(K – 1)}, или, говоря иначе, остаток R_{(K + 1)} стал бы нулем. Если же у нас спросят, почему процесс не может иметь последнего шага, то мы ответим, что в противном случае корень из 2 будет рациональным числом или, выражаясь геометрическим языком, диагональ квадрата будет соизмерима с его стороной, а это, добавим мы, абсурдно, ибо приводит к мысли о каких-то “четно-нечетных” числах. Однако, как явствует из сказанного выше, этот ход рассуждений, вполне естественный для современного человека, немыслим для раннего пифагорейца, поскольку уже предполагает знание о таком явлении, как несоизмеримость (= иррациональность), или по крайней мере требует явного выражения (АС) и (*1b). В конце концов, если бы древние греки могли рассуждать так, то о каком, собственно, кризисе математики могла бы идти речь?! И с чего бы это они стали называть диагональ квадрата “неприличной”?! Словом, для античных математиков, осуществляющих алгоритм Евклида для D и S, было необходимым наглядно и, так сказать, “в лоб” доказать, что эта процедура не может быть завершена, – только в этом случае они могли бы быть уверены, что диагональ квадрата несоизмерима с его стороной.

Теперь перед нами встает следующая проблема: возможно ли было для ранних пифагорейцев осуществить такое “прямое и наглядное” доказательство? Мы отвечаем на этот вопрос утвердительно, предъявляя способ, с помощью которого это можно было бы сделать даже на достаточно раннем этапе развития математики. Но чтобы прояснить нашу позицию, нам необходимо проделать некоторую предварительную работу.

Сначала мы приведем десятую теорему из второй книги “Элементов” Евклида [25]:

(Eвкл. II, 10) Дано: Γ – произвольная точка отрезка ΑΔ; Β – середина отрезка ΑΓ (рис. 4).

Рис. 4

Тогда: ΑΔ² + ΓΔ² = 2ΑΒ² + 2ΒΔ².

Заметим, что доказательство этой теоремы, приводимое Евклидом, вполне просто, оно опирается лишь на теорему Пифагора и некоторые несложные соображения [26]. Поэтому можно полагать, что пифагорейцы давно знали эту теорему.

Пойдем далее: в 27‑й главе “Комментария на Государство” Прокл Диадох сообщает, что пифагорейцам принадлежит “изящная теорема” (qeрrjma glafurиn), которая имеет следующую формулировку: “диагональ, присоединенная к стороне, диагональю которой она является, рождает [новую] сторону, а сторона, прибавленная сама к себе и присоединенная к ее диагонали, рождает [новую] диагональ” [27]. На более понятном нам языке эта “изящная теорема” звучит так:

(ИТ) Дано: S_М и D_М – отрезки, являющиеся соответственно стороной и диагональю (исходного или малого) квадрата.

Тогда: отрезки S_Б и D_Б, равные соответственно (S_М + D_М ) и (2S_М + D_М ), также являются соответственно стороной и диагональю (нового или большого) квадрата.

Доказательство (ИТ), приводимое Проклом и заимствованное им, по всей вероятности, из какого-то пифагорейского источника, опирается на частный случай (Eвкл. II, 10). Действительно, рассмотрим случай, когда отрезок ΓΔ является диагональю квадрата со стороной ΑΒ (= ΒΓ). Тогда имеем:

(i) ΑΔ² + ΓΔ² = 2ΑΒ² + 2ΒΔ² по (Eвкл. II, 10);

(ii) ΓΔ² = 2ΑΒ² по теореме Пифагора.

Подставляя (ii) в (i), получаем

(iii) ΑΔ² = 2ΒΔ².

Но последнее равенство как раз и означает, что отрезок ΑΔ является в нашем случае диагональю квадрата со стороной ΒΔ. Очевидно, кроме того, что ΒΔ = ΒΓ + ΓΔ, а ΑΔ = ΑΒ + ΒΓ + ΓΔ = 2ΑΒ + ΓΔ. С соответствующими вполне понятными переобозначениями имеем равенства “изящной теоремы”:

S_Б = S_М + D_М ;

(РИТ)

D_Б = 2S_М + D_М .

Итак, Пифагору было достаточно знать теорему (Eвкл. II, 10), чтобы получить “изящную теорему” вместе с соответствующими равенствами.

Более того, для получения (ИТ) и (РИТ) вовсе не обязательно располагать столь общим результатом, каким является (Eвкл. II, 10). Для доказательства “изящной теоремы” с ее равенствами достаточно, как легко заметить, простого чертежа, представленного на рис. 5.

Приведенные соображения, думается, более чем достаточно обосновывают наше мнение, что (ИТ) и (РИТ) вполне могли быть известны самым ранним пифагорейцам [28].

Рис. 5

Нам, однако, интересны не сами (ИТ) и (РИТ), а “симметричные” им результаты. Под “симметричностью” мы понимаем здесь следующее: (ИТ) говорит о переходе от исходного малого квадрата к новому большому, но ведь совершенно очевидно, что должен быть возможен и обратный переход – от исходного большого к новому малому. Так, должна быть справедлива

(ИТ*) Дано: S_Б и D_Б – отрезки, являющиеся соответственно стороной и диагональю (исходного или большого) квадрата.

Тогда: отрезки S_М и D_М , равные соответственно (D_Б – S_Б) и (2S_Б – D_Б), также являются соответственно стороной и диагональю (нового или малого) квадрата.

Выпишем также и равенства, соответствующие (ИТ*):

S_М = D_Б – S_Б;

(РИТ*)

D_М = 2S_Б – D_Б.

Переход от (ИТ) к (ИТ*), строго говоря, самоочевиден, поскольку (РИТ*) есть всего лишь другая форма записи (РИТ), т.е. две эти системы равенств совершенно равнозначны алгебраически. Тем не менее небесполезно будет представить некоторые обоснования того, что ранние пифагорейцы вполне могли знать (ИТ*).

Начнем с того, что у теоремы (Eвкл. II, 10) имеется, так сказать, “двойник”, – это девятая теорема из той же книги “Элементов”:

(Eвкл. II, 9) Дано: Β – середина отрезка ΑΔ; Γ – произвольная точка отрезка ΒΔ (рис. 6).

Рис. 6

Тогда: ΑΓ² + ΓΔ² = 2ΑΒ² + 2ΒΓ².

Можно сказать, что эта теорема также “симметрична” теореме (Eвкл. II, 10) примерно в том же смысле, в каком (ИТ*) симметрична (ИТ) [29]. Но для нас более важно, что доказательство (Eвкл. II, 9) совершенно аналогично доказательству (Eвкл. II, 10): в обоих рассуждениях используются одни и те же идеи, тождествен и смысл дополнительных построений. Словом, доказавший (Eвкл. II, 10) доказал и (Eвкл. II, 9).

Далее, мы помним, что (ИТ) доказывается из частного случая теоремы (Eвкл. II, 10), но ведь точно так же можно доказать и (ИТ*) из частного случая (Eвкл. II, 9). Действительно, рассмотрим случай, когда отрезок ΑΓ является диагональю квадрата со стороной ΑΒ (= ΒΔ). Тогда имеем

(i*) ΑΓ² + ΓΔ² = 2ΑΒ² + 2ΒΓ² по (Eвкл. II, 9);

(ii*) ΑΓ² = 2ΑΒ² по теореме Пифагора.

Подставляя (ii) в (i), получаем

(iii*) ΓΔ² = 2ΒΓ².

Но (iii*) как раз и означает, что отрезок ΓΔ является в нашем случае диагональю квадрата со стороной 2ΒΓ. Очевидно, кроме того, что ΒΓ = ΑΓ – ΑΒ, а ΓΔ = ΑΒ + ΒΔ – ΑΓ = 2ΑΒ – ΑΓ. Отсюда, с соответствующими переобозначениями, имеем (РИТ*).

Отметим также и то обстоятельство, что для получения (ИТ*) и (РИТ*) не обязательно, вообще говоря, знание (Eвкл. II, 9), – достаточно, опять-таки, лишь более внимательного взгляда на рис. 5. Итак, опираясь на вышесказанное, мы приходим к вполне обоснованной гипотезе: даже на довольно раннем этапе развития математики было возможно вполне строгое геометрическое доказательство (ИТ*).

Теперь вернемся к алгоритму Евклида, осуществляемому для диагонали и стороны квадрата, которые мы для удобства обозначим сейчас соответственно через D₀ и S₀. Используя запись (АЕ₀), совершаем 0‑й шаг процедуры: смотрим, сколько раз сторона S₀ укладывается в диагональ D₀, т.е. ищем N₀, и то, каков будет “остаток”, т.е. R₀. Очевидно, что N₀ будет равно 1, а R₀ можно записать как (D₀ – S₀). А теперь вспомним первое равенство (РИТ*): наш остаток (D₀ – S₀) совпадает со стороной того малого “производного” квадрата, о котором говорит (ИТ*), – поэтому обозначим остаток через S₁. Итак, в нашем конкретном случае (АЕ₀) запишется как

(Ш₀) D₀ = S₀ + S₁.

Перейдем к следующему шагу: спрашивается, сколько раз “новая” сторона S₁ (= D₀ – S₀) укладывается в “старую” сторону S₀, т.е. каково N₁ и каков “остаток” R₁. Несложно показать, например из рис. 5 или из (Eвкл. II, 9), что N₁ = 2. Отсюда легко находится R₁: R₁ = S₀ – 2S₁ = (S₀ – – S₁) – S₁ = (S₀ – (D₀ – S₀)) – S₁ = (2S₀ – D₀) – S₁. А теперь вспомним второе равенство (РИТ*): отрезок (2S₀ – D₀) совпадает с диагональю малого “производного” квадрата, – поэтому обозначим его через D₁. Следовательно, R₁ = (D₁ – S₁), но ведь если применить (ИТ*) теперь уже к новому квадрату – квадрату со стороной S₁, то отрезок (D₁ – S₁), согласно первому равенству (РИТ*), будет стороной второго “производного” квадрата – квадрата еще более малого. Поэтому R₁ = S₂, а (АЕ₁) запишется как

(Ш₁) S₀ = 2S₁ + S₂.

Стоит пойти еще чуть далее и задать себе вопрос: сколько раз “вторая новая” сторона S₂ (= D₁ – S₁) укладывается в “первую новую” сторону S₁, т.е. каково N₂ и каков “остаток” R₂? А после этого вопроса становится ясным, что “идти далее” уже нет смысла, ибо этот шаг будет точной копией предыдущего, – размеры соответствующих отрезков, т.е. длины новых “исходных” и новых “производных” сторон и диагоналей, конечно, уменьшились, но соотношение между исходным и производным квадратами, задаваемое теоремой (ИТ*) или равенствами (РИТ*), осталось тем же самым. Поэтому данный шаг опишется формулой

(Ш₂) S₁ = 2 S₂ + (D₂ – S₂) = 2S₂ + S₃.

И все остальные шаги будут, очевидно, точно такими же: “новая” сторона будет укладываться в “старой” дважды, давая в остатке “еще более новую сторону”, или, что то же самое, разность между “новой” стороной и “новой” диагональю. Тем самым для произвольного I‑го шага (i ³ 1) будет верна формула

(Ш_i) S_(i -1) = 2S_i + (D_i – S_i) = 2S_i + S_(i +1).

Становится очевидным, что наша процедура никогда не закончится: ведь невозможно же, чтобы разность диагонали и стороны квадрата (сколь угодно малого) равнялась нулю. Но если наша процедура не может завершиться, то невозможно, следовательно, найти отрезок, соизмеряющий сторону и диагональ квадрата. Итак, мы представили прямое и непосредственное доказательство того факта, что сторона и диагональ квадрата суть несоизмеримые отрезки.

Еще раз подчеркнем, что предлагаемая нами реконструкция открытия античными математиками несоизмеримости базируется на довольно-таки тривиальных геометрических соображениях и рассуждениях. Такой ход мысли был вполне по плечу Пифагору или кому-то из его ранних последователей [30]. Заканчивая этот раздел, нам осталось лишь ответить на возможный упрек в излишней “алгебраичности” применения алгоритма Евклида к стороне и диагонали квадрата. Разумеется, форма рассуждений у античных математиков была значительно более “геометрической”. Мы предпочли другой путь как из соображений удобства пояснений, так и по техническим причинам. Весьма несложно, однако, переложить все эти рассуждения на чистый “язык чертежей”.

Кризис после кризиса

Доказав существование несоизмеримых отрезков, “чистый” математик мог бы быть доволен, поскольку этим преодолевался кризис основ его науки. Для пифагорейца же такое разрешение коллизии означало наступление нового, еще более жесткого кризиса: доказательство существования несоизмеримых величин наносило тяжкий удар по одному из важнейших пунктов пифагорейской философии, т.е. по тезису “единица – начало всего”. Действительно, “неприличная” диагональ квадрата несоизмерима с единичной стороной и в этом смысле несводима к ней, а если дело обстоит таким образом, то можно ли утверждать, что единица “начальствует” над диагональю или как-то “начинает” ее?! Или, быть может, единица не является все-таки универсальным началом?

В этой ситуации более изощренная мысль стала бы, по всей видимости, проводить более четкую грань между наукой и философией, между положениями первой и догматами последней, но для пифагорейцев всех времен этот путь был не столь хорош, – математика слишком уж грубо и конкретно была “прописана” в их философии. Пифагорейцы нашли, по нашему мнению, иной выход из положения: они смогли достаточно изящно перетолковать соизмеримость и “начальственную” роль единицы таким образом, чтобы мистическая монада “начинала” также и “неприличную” диагональ. Это перетолкование носит, естественно, математический характер и свидетельствует, на наш взгляд, о дальнейших успехах пифагорейской математики.

До наших дней дошел трактат Теона Смирнского (I–II вв. н.э.) “О математическом, полезном при чтении Платона”, состоящий из трех частей, в которых излагаются соответственно пифагорейская теория чисел, теория музыки и астрономическая теория [31]. Наиболее ценны две последние части, поскольку содержание первой во многом дублирует “Введение в арифметику” Никомаха Геразского (I в. до н.э. – I в. н.э.). Однако и в первой части содержатся некоторые сведения, которых нет у Никомаха, – такова интересующая нас главка “О сторонних и диагональных числах”, которую более или менее подробно комментировали многие выдающиеся историки математики (Г.Нессельман, М.Кантор, П.Таннери, Ф.Гульч, Г.Цейтен, М.Я.Выгодский, Б.Ван дер Варден и др.) [32].

Сначала приведем наиболее важный для нас фрагмент [33]:

Ведь так же, как все фигуры (scjmЂtwn) [= числа]… начинает (€rcei) единица [34], так и отношение диагонали и стороны [квадрата] [35] отыскивается при помощи единицы (ќn tЮ monЂdi) [36]. Вот берутся (oµon ќkt°qentai) [37] две единицы, из которых одна назначается нами (fтmen eєnai) “диагональю”, а другая – “стороной”, ибо единица, будучи началом (‡rcРn) всего, должна быть в возможности (dunЂmei) и стороной, и диагональю. И прибавляется к “стороне” “диагональ”, к “диагонали” же – две “стороны”… И у первой “стороны” и “диагонали” квадрат на единице “диагонали” [38] одной единицей меньше двойного квадрата на единице “стороны”. <…> Прибавляем к “стороне” “диагональ”, то есть единицу к единице; тогда [вторая] “сторона” будет из двух единиц. К “диагонали” же прибавляем две стороны, то есть к единице две единицы; [вторая] “диагональ” будет из трех единиц. И квадрат на стороне-двойке есть 4; квадрат же на стороне-тройке – 9. Итак, квадрат 9 единицей больше двойного квадрата на стороне-двойке. Опять прибавляем к [второй] “стороне” 2 [вторую] “диагональ”-тройку; [третья] “сторона” будет 5; к “диагонали” же тройке – две “стороны”, то есть два раза по два; [третья “диагональ”] будет 7. <…> И от следующих одна за другой (›zТv) прибавок, подобных этим, будет то же попеременно: то квадрат на “диагонали” единицей меньше двойного квадрата на “стороне”, то единицей больше. И такие “стороны” и “диагонали” соизмеримы (їjta±) [39].

Сделаем теперь несколько замечаний. Во-первых, текст главки “О сторонних и диагональных числах”, особенно если брать его целиком, производит неприятное впечатление своей неясностью и какой-то “герметичностью” (о неясности этого текста писал еще Г.Нессельман [40]), поэтому можно понять М.Я.Выгодского, который сетует на “мистическую шелуху” и «“глубокомысленные” метафизические доводы» [41]. Во-вторых, текст Теона явно описывает некий алгоритм, который описывается еще и Проклом в 23‑й главе “Комментария на Государство”, причем Прокл сообщает, что этот алгоритм принадлежит пифагорейцам [42]. Очевидно, в-третьих, что этот пифагорейский алгоритм (ПА), говоря современным языком, состоит в построении двух рекуррентных последовательностей (“стóроны” и “диагонали” – S_n и D_n) и задается следующими условиями:

S_n+1 = S_n + D_n;

(ПА) //S₁ =1, D₁ =1, n = 1, 2, 3…//

D_n+1 = 2S_n + D_n.

В-четвертых, описывая (ПА), Теон обращает наше внимание на то, что

(#) 2S_n² – D_n² = (-1)^n +1.

Не располагая понятием отрицательного числа, он формулирует это так: «…От следующих одна за другой прибавок, подобных этим, будет то же попеременно: то квадрат на “диагонали” единицей меньше двойного квадрата на “стороне”, то единицей больше». “И всегда так”, – говорит Прокл о равенстве (#) в своем описании (ПА) [43]. Спрашивается, в-пятых, для чего нужен (ПА)?

На этот вопрос большинство историков науки отвечают так: для приближенного вычисления корня из 2, т.е. для приближенного вычисления отношения диагонали квадрата к его стороне, – именно поэтому в нашем переводе иногда говорится об условных “сторонах” и “диагоналях”, а иногда – о настоящих сторонах и диагоналях (без кавычек) [44]. Действительно, организовав последовательность отношений “диагоналей” к соответствующим “сторонам” – А_n = D_n/S_n – и учитывая равенство (#), легко показать, что А_n стремится к корню из 2. И в этом смысле, действительно, “отношение диагонали и стороны [квадрата] отыскивается при помощи единицы”, как говорит Теон в начале цитированного фрагмента.

Как пишет М.Я.Выгодский, “Теон Смирнский не дает никакого доказательства излагаемому им процессу” [45], но такое доказательство явно должно было существовать. Чтобы показать, что с помощью (ПА) действительно можно соизмерить сторону и диагональ квадрата, достаточно лишь обосновать равенство (#), – остальное будет уже лишь “делом техники” [46]. Но как же это сделать? Пытаясь ответить на этот вопрос, можно обратить внимание на “подозрительное” сходство равенств (ПА) и (РИТ). Более того, как легко заметить по примечаниям, Прокл сообщает об (ИТ) как раз в рамках обсуждения (ПА) и даже заканчивает доказательство (ИТ) словами “и к этому еще то же самое таким же образом” [47], т.е. рассматривает “изящное” построение производного квадрата как рекуррентную процедуру. Конечно, равенство (#) нельзя обосновать через (РИТ) непосредственно из-за различий в условиях, но это можно сделать с помощью (Eвкл. II, 10), на которой Прокл базирует доказательство (ИТ) [48].

Действительно, если рассмотреть частный случай (Eвкл. II, 10), когда ΑΒ = ΒΓ = S₁ (=1), а ΓΔ = D₁ (=1), то получим равенство

(2S₁ + D₁)² + D₁² = 2S₁² + 2(S₁ + D₁)².

Учитывая реккурентные условия (ПА), это равенство можно записать как

D₂² + D₁² = 2S₁² + 2S₂²

или, после элементарных преобразований, как

2S₁² – D₁² = D₂² – 2S₂².

Но если теперь рассмотреть частный случай (Eвкл. II, 10), когда
ΑΒ = ΒΓ = S₂ (= 2), а ΓΔ = D₂ (= 3), то получим, опуская промежуточные действия, равенство

D₂² – 2S₂² = 2S₃² – D₃².

Очевидно, что рассмотрение таких частных случаев (Eвкл. II, 10) можно продолжать и далее, поэтому имеем следующее “бесконечное” равенство:

…= D₄² – 2S₄² = 2S₃² – D₃² = D₂² – 2S₂² = 2S₁² – D₁² =

= [так как S₁ =1, D₁ =1] = 1,

которое есть лишь другая форма записи для равенства (#). Поскольку же мы показали истинность (#), постольку мы обосновали тот факт, что (ПА) дает нам такие “диагонали” и “стороны” (D_n и S_n), отношение которых друг к другу (А_n = D_n/S_n) бесконечно приближается к соотношению диагонали и стороны квадарата [49].

Создание (ПА) само по себе является, конечно же, выдающимся математическим достижением, но мы сейчас говорим не столько о математике, сколько о философии – о кризисе пифагореизма, возникшем по причине преодоления математического кризиса. Поэтому здесь значительно более важна та философская интерпретация данного научного результата, которую ему давали пифагорейцы. Вспомним, что говорит Теон: “…Так же, как все фигуры [= числа]… начинает единица, так и и отношение диагонали и стороны [квадрата] отыскивается при помощи единицы… ибо единица, будучи началом всего, должна быть в возможности и стороной, и диагональю”. Затем, построив рекуррентные последовательности D_n и S_n, он отмечает, что «такие “стороны” и “диагонали” соизмеримы». В самом деле, можно сказать, что единица является первым членом (= “началом”) обеих последовательностей, соотношение членов которых стремится к корню из 2, и в этом смысле можно сказать, что диагональ квадрата “соизмерима” со стороной и что единица является “началом” диагонали. Такая интерпретация (ПА) вполне позволяет сохранить тезис “единица – начало всего” и дает пифагорейское объяснение такому “неприятному” явлению, как несоизмеримость отрезков.

Сказанное выше вполне корректно, по нашему мнению, дополнить еще и такими соображениями. Широко известно высказывание Аристотеля о том, что “бесконечность не может быть завершенной” (Физ. 204а). Кстати говоря, данное мнение (вкупе с проистекающими из него следствиями) получило широчайшее распространение в европейской мысли. Например, “король математиков” К.Гаусс полагал, что «употребление бесконечной величины как “завершенной” никогда не будет разрешено в математике» [50]. Но Аристотель знает, что не все разделяют его убеждение: “…Пифагорейцы… рассматривают бесконечность саму по себе, считая ее… самостоятельной (и, следовательно, завершенной. – Е.К.) сущностью” (Физ. 203а). Сохранились, кроме того, многочисленные отрывки, свидетельствующие о том, что бесконечность являлась у пифагорейцев одним из “начал” всего сущего [51]. Если учесть все это, то напрашивается догадка, что пифагорейцы, открывшие (ПА), мыслили свой бесконечный алгоритм “завершенным” [52].

Теперь представим античного математика, который принимает подобную мысль. Ведь он, обосновывая тезис “единица – начало всего”, может сказать, что диагональ и сторона квадрата “соизмеримы в бесконечности”, или нечто подобное – и будет по-своему прав. Более того, текст Теона гораздо удобнее читать, если представлять себе бесконечную последовательность ромбов со стороной S_n, у которых одна из диагоналей равняется D_n. Если считать эту последовательность “завершенной”, то будет существовать некий “бесконечный квадрат”, стороны и диагональ которого являются совокупностью единичных отрезков и, следовательно, соизмеримы. Но ведь любой квадрат подобен единичному, следовательно, и бесконечный. А это значит, что и у единичного квадрата диагональ можно считать соизмеримой стороне.

Заключение

По поводу сказанного в этой статье можно задать много вопросов, но далеко не на все из них автор мог бы дать ответы, – это касается в особенности раздела “Кризис после кризиса”. Так, например, интересен вопрос о том, когда пифагорейцы открыли (ПА) [53]. Существует также масса вопросов о различного рода деталях этого замечательного открытия.

Для нас интересны и следующие размышления: если представить, что пифагорейцы открыли (ПА), имея в виду понятие актуальной бесконечности, а мы полагаем, что так и было, то тогда философские трудности, связанные с первым кризисом оснований математики, были разрешены пифагорейцами на таком уровне, что разрешение, скажем, второго кризиса (создание теории пределов для обоснования интегро-дифференциального исчисления) было, в принципе, лишь делом техники. Более того, они были разрешены так, что понятие актуальной бесконечности могло бы войти в математику задолго до Г.Кантора, а ведь речь идет уже об одном из важных аспектов третьего кризиса!

Что же касается финальных – по задачам – выводов статьи, то они, как нам кажется, излишни в силу достаточной ясности сказанного в соответствующих ее разделах.

Примечания

1. Сразу отметим, что у исследователей нет единодушия в вопросах о вкладе в развитие математики раннего пифагореизма и лично Пифагора. Так, представители гиперкритического направления (см., например: Burkert W. Weisheit und Wissenschaft: Studen zu Pythagoras, Philolaos und Platon. – Nürnberg, 1962; Frank E. Plato und die sogenannten Pythagoreer. – Darmstadt, 1962) утверждают, что древние пифагорейцы, в том числе и сам Пифагор, математикой, строго говоря, не занимались и что до трудов Архита Тарентского (ок. 400 г. до н.э.) говорить о пифагорейской математике не имеет смысла. Однако далеко не все исследователи, как отечественные, так и зарубежные, столь недоверчивы к рассказам неопифагорейцев и неоплатоников (см., например: Ван дер Варден Б.Л. Пробуждающаяся наука. – М., 1959; Выгодский М.Я. Арифметика и алгебра в древнем мире; Нейгебауер О. Точные науки в древности. – М., 1968). “Достаточно показателен тот факт, что уже в конце V в. до н.э. Гиппократ Хиосский составил руководство по геометрии (трактат “Элементы”, не дошедший до нас. – Е.К.), написанное в том же духе, что и позднейшие работы математиков IV в. Вся предварительная работа по доказательству теорем… была выполнена пифагорейскими математиками меньше чем за сто лет. О деталях работы мы ничего не знаем, но ее начало, как можно думать, было положено Пифагором” (Рожанский И.Д. Ранняя греческая философия // Фрагменты ранних греческих философов (далее – ФРГФ) / Под ред. А.В.Лебедева. – М., 1989. – Ч. 1. – С. 15).

2. Под этим мы понимаем не конкретную гетерию в Кротоне (или каком-то другом городе), но “содружество” пифагорейцев всей Греции.

3. См.: ФРГФ 18, 4–4а.

4. См.: ФРГФ 18, 2.

5. Мы увидим данное высказывание в отрывке Теона Смирнского, но уже Аристотель (см., например, Мет. 985b) передает мнение пифагорейцев, что “числа первичны по отношению ко всей природе”. Поскольку же греческое слово ‡riqmзv (число) означает натуральное число, постольку единица, будучи “началом” натуральных чисел (см.: Евклид. Элем. VII, 1), является и началом всего сущего. См. также комментарий Александра Афродисийского к указанному месту “Метафизики” (ФРГФ. – С. 469).

6. Неправильно было бы думать, что две эти взаимосвязанные задачи слишком тривиальны. Наше общее впечатление таково, что большинство историков науки просто не замечают глубинной сути данных вопросов и по этой причине дают на них весьма поверхностные ответы.

7. Мы полагаем так хотя бы из чувства противоречия: обычная (и совершенно неверная, по нашему мнению) зарисовка первого кризиса предполагает, как правило, обратный порядок (см. далее).

8. Отсюда ясно, что автор данной статьи во многом доверяет сообщениям Порфирия, Ямвлиха и Прокла. Помимо соображений И.Д.Рожанского, приведенных в прим. 1, мы можем сослаться также и на свидетельство Эвдема из его “Истории геометрии”, которое сохранились у Прокла в “Комментариях к Евклиду”: “Пифагор преобразовал занятия геометрией… изучая ее высшие основания и рассматривая теоремы абстрактно (‡Аlwv = нематериально) и ноэтически” (Procli Diadochi in primum Euclidis elementorum librum commentarii / Rec. G.Fridlein. – Lipsiae, 1873. – P. 65).

9. Отрезки называются соизмеримыми, если имеется такой отрезок, который укладывается в каждый из них целое число раз. Говоря более формально, отрезки α и β соизмеримы Û_df ($ отрезок γ) ($ m, n Î N) ((α = mγ) & (β = nγ)).

10. Мы не приводим это рассуждение, считая его известным из школьного курса математики.

11. (АС) возникает, видимо, вследствие неосознанного обобщения обыденной практики, ведь чисто практически данное положение работает! Поэтому, кстати, пифагорейский тезис “единица – начало всего” можно считать результатом рефлексии над содержанием обыденного сознания. Тем, кто не верит, что обыденный “здравый смысл” принимает (АС) за истину, советуем провести небольшой опрос школьников и людей, недавно закончивших школу (но не профессиональных математиков!). Заметим, что автор сам был просто поражен, проведя такой опрос.

12. Здесь более корректно, вообще говоря, вести речь о поле алгебраических чисел.

13. Диагональ квадрата была обозначена греками, как известно, весьма показательным словом €Пїjtj, т.е. ее воспринимали именно ужасной, неприличной, непозволительной или немыслимой (употребляемый сейчас латинизм “иррациональность” также напоминает о немыслимости, хотя и восходит, по всей видимости, к другому значению слова ratio – “отношение, (со)измерение”). В указанном греческом термине мы видим, кстати, некоторое косвенное подтверждение нашего мнения о том, что именно открытие теоремы Пифагора привело к возникновению первого кризиса математики.

14. Рожанский И.Д. Ранняя греческая философия. – С. 15.

15. Это, впрочем, вовсе не означает, что вавилонские математики располагали доказательством теоремы Пифагора, а ведь без доказанного и тем самым “осознанно необходимого” результата кризис не должен был состояться. И здесь бесполезны ссылки на простейший случай теоремы Пифагора, очевидный из рис. 1 и 2, поскольку вавилоняне в отличие от греков отнюдь не были прирожденными геометрами, их математика изначально носила “арифметико-алгебраический” характер.

16. Юшкевич А.П. [Предисловие] // Нейгебауер О. Точные науки… – С. 8. Если для кого-либо все эти соображения (см. также прим. 15) недостаточны, то нам остается лишь констатировать следующее: “даже если только из-за неполноты нашего знания источников мы предполагаем, что вавилоняне не знали, что уравнение p² = 2q² не имеет решения в целых числах, то и тогда остается несомненным, что последствия этого результата не были осознаны” (Нейгебауер О. Точные науки… – С. 62).

17. Юшкевич А.П. [Предисловие] – C. 8.

18. Цит. по: Procli Diadochi in primum Euclidis… – P. 65.

19. Паев М.Е. Решение двух античных проблем. – Киев, 1987. – С. 203.

20. ФРГФ 44 В, 5.

21. См.: Евклид. Элем. X, 2. Алгоритм Евклида изучается в школе как способ нахождения наибольшего общего делителя двух чисел.

22. Набор {N_i} есть, разумеется, набор натуральных чисел.

23. Процесс прервется, конечно же, лишь в том случае, если отрезки α и β соизмеримы.

24. Причем γ, как легко показать, будет наибольшим соизмеряющим отрезком.

25. Как эту теорему, так и 9‑ю теорему из той же книги “Элементов”, мы приводим, полностью сохраняя геометрический смысл, но в более удобных и более точных, с нашей точки зрения, формулировках.

26. Алгебраическое же доказательство этой теоремы и вовсе тривиально.

27. Procli Diadochi in Platonis Rem Publicam commentarii / Ed. G.Kroll. – Lipsiae, 1901. – V. 2. – P. 27, 28.

28. Алгебраическое доказательство (ИТ) совершенно тривиально.

29. Точнее говоря, эти две теоремы “симметричны” так же, как “симметричны” выражения (2a + b)² + b² = 2a² + 2(a + b)² и (2a – b)² + b² = 2a² + 2(a – b)².

30. Ясно, тем не менее, что создание и даже восприятие такого рода рассуждений требует, конечно же, некоторой подготовки. Поэтому мы не думаем, что всякий образованный древний грек был обязан знать о “теории несоизмеримых”. Например, как сообщает Прокл, атомисты Ксенократ и Эпикур отрицали даже само существование несоизмеримых отрезков (см.: Procli Diadochi in Platonis Rem Publicam… – Р. 27).

31. Под индексом 307(А) в венецианской библиотеке св. Марка хранится греческая рукопись XI или XII в., найденная в XVI в. Заглавие этой рукописи таково: Q™wnov Smurna°ou PlatwnikoВ tтn katЂ tи maqjmatikиn crjs°mwn e°v tРn PlЂtwnov ‡nЂgnwsiv. Она содержит, однако, лишь две первые части сочинения Теона и была издана в 1644 г. в Париже астрономом Измаилом Буйо (Bullialdus) под заглавием “Theonis Smyrnaei Platonici expositio eorum, quae in mathematicis ad Platonis lectionem utilia sunt”. Третья, астрономическая, часть трактата была найдена позже в Миланской библиотеке св. Амвросия, а затем и в библиотеке св. Марка (рукопись 303(В) XIV или XV вв.). Единственное, насколько мы знаем, полное издание трактата –“Theonis Smyrnaei philosophi platonici expositio rerum mathematicarum ad legendum Platonem utilium” (Rec. E.Hiller. – Lonsiae, 1878).

32. Первым обратил внимание на эту главку Г.Нессельман в своей книге “Die Algebra der Griechen”, изданной в середине XIX в. Ее перевод на русский язык впервые осуществил М.Я.Выгодский (см.: Выгодский М.Я. Арифметика… – С. 317, 318). Еще один перевод этой главки принадлежит М.Е.Паеву (см.: Паев М.Е. Решение… – С. 61). Перевод М.Е.Паева свободен от многих явных неточностей, встречающихся у М.Я.Выгодского,
и более адекватно, по нашему мнению, передает мысль Теона. Однако мы не можем полностью согласиться с теми смелыми толкованиями и реконструкциями, которые М.Е.Паев присовокупляет к своему переводу.

33. Мы опускаем сопровождающие текст рисунки Теона, которые не играют особой роли, и передаем арабскими цифрами греческие “буквенные” обозначения чисел. “Навешивание” на некоторые слова кавычек, которых, разумеется, нет в греческом тексте, будет разъяснено далее.

34. Или: “над всеми фигурами… начальствует единица” (см. у М.Я.Выгодского). Такой перевод возможен, но затрудняет чтение. В тексте речь, кроме того, идет о некотором процессе, начинающемся с единицы. Что касается оборота “все фигуры [= числа]… начинает единица”, то имеется в виду пифагорейская манера, известная нам по сообщениям Никомаха и Теона, представлять числа в виде точечных структур. Число же Теон определяет как “соединение единиц… c единицы начинающееся (‡pи monЂdov arcзmenov)” (Theonis Smyrnaei philosophi… – P. 183; ср.: Евклид. Элем. VII, 1).

35. В тексте: tТv diam™trou ka° tТv pleur‚v lзgov. М.Е.Паев полагает, что здесь идет речь о двух отношениях (диагонали и стороны) к единичному отрезку, т.е. о соизмеримости стороны и диагонали с единицей. Возможно, он прав, но возможно и наше прочтение (говорится об отношении диагонали к стороне).

36. Здесь, несомненно, инструментальный дательный, а не локатив. Перевод “отыскивается в единице” (см. у М.Я.Выгодского) был бы именно “мистической шелухой” (см.: Выгодский М.Я. Арифметика… – С. 319), но мы никогда не слышали, что пифагорейцы что-то “искали в единице”.

37. Букв.: “так [= вот] выставляются напоказ”. Это может означать, что приводится конкретный пример для теории общего характера, – поэтому есть возможность того, что Теон говорит не просто о диагонали квадрата, но о диагонали произвольного прямоугольника. М.Е.Паев категорически утверждает, что дело обстоит именно так (см.: Паев М.Е. Решение… – С. 64 и далее). С нашей же точки зрения, текст Теона не располагает к категоричности.

38. Имеется в виду, что первая диагональ (и, далее, первая сторона) равна единице по длине.

39. Theonis Smyrnaei philosophi… – Р. 42–44.

40. См.: Паев М.Е. Решение… – С. 56.

41. См.: Выгодский М.Я. Арифметика… – С. 319.

42. См.: Procli Diadochi in Platonis Rem Publicam… – Р. 24, 25, 28, 29. Небезынтересно заметить, что этот процесс построения “сторон” и “диагоналей” мог явиться, по мнению известного историка математики И.Гофмана, источником важных идей для П.Ферма в связи с его знаменитым уравнением ax² + 1 = y² (см.: Hoffman J.E. Ergдnzende Bemerkungen zum “geometrischen” Irrationalitätsbeweis der alten Griechen // Centaurus. – 1956. – V. 5, № 1. – P. 63).

43. Procli Diadochi in Platonis Rem Publicam… – Р. 29.

44. См.: Ван дер Варден Б.Л. Пробуждающаяся наука. – С. 117; Выгодский М.Я. Арифметика… – С. 317; Цейтен Г.Г. История математики в древности и в средние века. – М., 1938. – С. 51, 52.

45. См.: Выгодский М.Я. Арифметика… – С. 319.

46. Разделим равенство (#) на D² и перейдем к пределу.

47. Procli Diadochi in Platonis Rem Publicam… – Р. 28.

48. Нам непонятно, почему М.Я.Выгодский и Б.Л.Ван дер Варден отрицают это (см.: Ван дер Варден Б.Л. Пробуждающаяся наука. – С. 116 и след.; Выгодский М.Я. Арифметика… – С. 319 и след.).

49. То есть квадрат на “диагонали” D_n асимптотически “превращается” в двойной квадрат “стороны” S_n.

50. Цит. по: Maracchia S. La fama “immeritata” di Enopide di Chio Archimede. – P., 1978. – P. 70.

51. См., например: ФРГФ 44 А, 9.

52. В связи со сказанным стоит отметить мнение (см.: Maracchia S. La fama… – P. 68–76), что понятие актуальной бесконечности скрыто используется в некоторых частях “Элементов” Евклида (см. I, 12 и I, 22).

53. Возможно, очень рано знали об этом открытии – возможно, уже Платон. Во всяком случае, в таком духе можно проинтрепретировать так называемую “речь муз” в “Государстве” (см.: Камельчук Е.Н. Платон и “совершенное число (лет) для бракосочетания” // Логика и приложения: Тез. междунар. конф. – Новосибирск, 2000).

Институт философии и права

СО РАН, Новосибирск

Kamelchuk, E.N. The first crisis of grounds for mathematics, and Pythagorean philosophy

The paper presents a cross-disciplinary study carried out at the interface of history of science, philosophy of science and history of philosophy. Mathematical and philosophical aspects of the first crisis of principles for mathematics are considered. The problem of the essence of this crisis and definite historical circumstances under which it arose is discussed; the idea that it is necessary to provide a direct proof for existence of incommensurable segments is stated. Further, the author offers a reconstruction of means by which ancient mathematicians overcame the crisis of their science; he points out the discrepancy between the existence of irrational figures and principles for Pythagorean philosophy. He also shows that Pythagoreans coped perfectly with the “crisis of principles” for their philosophy which was a result of a successful settlement of mathematical crisis.